آموزش مساحت مثلث 0 تا 100 انواع آن+ PDF و 12 نمونه سوال

مثلث یکی از بنیادی‌ترین اشکال هندسی است که در علوم مختلف از جمله ریاضیات، مهندسی، معماری و حتی هنر نقش مهمی ایفا می‌کند. یادگیری نحوه محاسبه مساحت مثلث نه‌تنها برای موفقیت در درس ریاضی ضروری است، بلکه به دانش‌آموزان کمک می‌کند تا مسائل دنیای واقعی مانند محاسبه مساحت زمین یا طراحی سازه‌ها را حل کنند.

 این مقاله با هدف ارائه یک راهنمای جامع، ساده و کاربردی طراحی شده است تا دانش‌آموزان در هر سطحی، حتی بدون دانش قبلی، بتوانند مساحت مثلث را به‌طور کامل درک کنند. از تعریف مثلث و انواع آن تا فرمول‌های دقیق و مثال‌های عملی، این مقاله تمام جنبه‌های موضوع را پوشش می‌دهد تا هیچ سؤالی برای خواننده باقی نماند.

مثلث، ساده‌ترین چندضلعی با سه ضلع، سه زاویه و سه رأس است که مجموع زوایای داخلی آن همیشه 180 درجه است. مساحت مثلث، که سطح محصور شده توسط اضلاع آن را نشان می‌دهد، در موقعیت‌های مختلفی مانند طراحی، برنامه‌ریزی شهری و محاسبات مهندسی کاربرد دارد. این مقاله با ساختاری منظم و زبانی ساده، به دانش‌آموزان کمک می‌کند تا با انواع مثلث‌ها، روش‌های محاسبه مساحت و کاربردهای آن آشنا شوند.

دنیای ساده مثلث

مثلث یک شکل هندسی بسته است که از اتصال سه پاره‌خط غیرهم‌راستا در سه نقطه (رأس) تشکیل می‌شود. این شکل دارای سه ضلع، سه زاویه و سه ارتفاع است. ارتفاع، خطی عمود است که از یک رأس به ضلع مقابل (قاعده) یا امتداد آن رسم می‌شود.

هر ضلع می‌تواند به‌عنوان قاعده در نظر گرفته شود، و ارتفاع متناظر با آن، خط عمود بر آن ضلع است. مثلث‌ها به دلیل ساختار ساده و پایدارشان، پایه بسیاری از محاسبات هندسی هستند و در اشکال پیچیده‌تر می‌توانند به چند مثلث تقسیم شوند تا محاسبه مساحت آسان‌تر شود.

انواع مثلث‌ها

مثلث‌ها بر اساس طول اضلاع و اندازه زوایای داخلی به دسته‌های مختلفی تقسیم می‌شوند. شناخت این انواع برای انتخاب روش مناسب محاسبه مساحت ضروری است:

هر نوع مثلث ممکن است نیاز به روش خاصی برای محاسبه مساحت داشته باشد که در ادامه توضیح داده خواهد شد.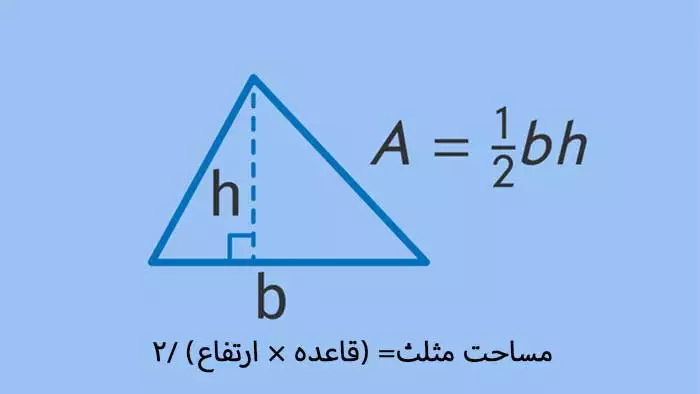
مساحت مثلث = قاعده ضربدر ارتفاع و بعد عدد بدست آمده را تقسیم بر 2 کنید

فرمول اصلی محاسبه مساحت مثلث

رایج‌ترین فرمول برای محاسبه مساحت مثلث، فرمول قاعده و ارتفاع است که برای همه انواع مثلث‌ها قابل استفاده است:

مساحت = ½ × قاعده × ارتفاع

در این فرمول، قاعده یکی از اضلاع مثلث است و ارتفاع، خط عمود از رأس مقابل به قاعده یا امتداد آن است. این فرمول به دلیل سادگی برای دانش‌آموزان در مقاطع مختلف مناسب است. برای مثال، اگر قاعده مثلثی 8 سانتی‌متر و ارتفاع آن 5 سانتی‌متر باشد:

مساحت = ½ × 8 × 5 = 20 سانتی‌متر مربع

این فرمول پایه‌ای است و در بسیاری از مسائل، حتی با اطلاعات محدود، قابل استفاده است.

روش‌های مختلف محاسبه مساحت مثلث

علاوه بر فرمول اصلی، روش‌های دیگری نیز برای محاسبه مساحت مثلث وجود دارند که بسته به اطلاعات موجود در مسئله استفاده می‌شوند. این روش‌ها به دانش‌آموزان امکان می‌دهند تا در موقعیت‌های مختلف، مساحت را به‌راحتی محاسبه کنند.

فرمول هرون

هنگامی که طول سه ضلع مثلث (a، b، c) مشخص باشد، فرمول هرون بهترین گزینه است:

محیط نیمه (s) را محاسبه کنید:

s = (a + b + c) ÷ 2

مساحت را با فرمول زیر به دست آورید:

مساحت = √[s × (s - a) × (s - b) × (s - c)]

مثال:

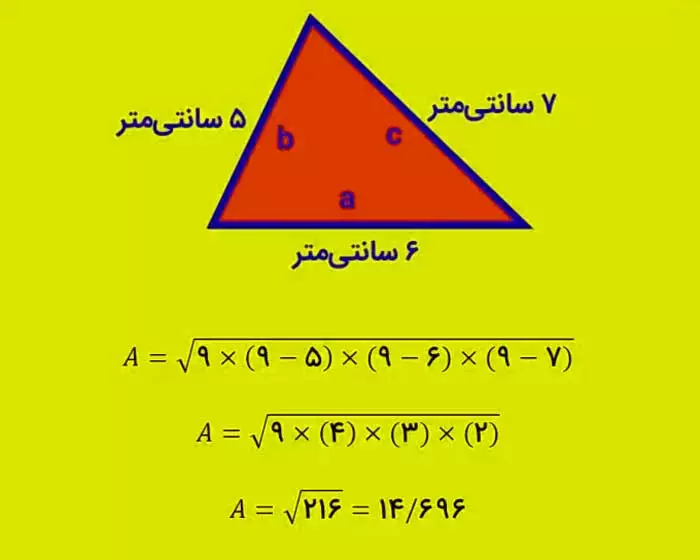
این روش برای مثلث‌هایی که قاعده و ارتفاع مشخص نیست، بسیار کاربردی است.

بلد باشید:  مساحت و محیط مثلث----مساحت و محیط مربع ----مساحت و محیط ذوزنقه 

روش مثلثاتی (دو ضلع و زاویه بین آن‌ها)

اگر طول دو ضلع (a و b) و زاویه بین آن‌ها (C) مشخص باشد، از فرمول زیر استفاده می‌شود:

مساحت = ½ × a × b × sin(C)

این روش برای مسائل شامل اطلاعات زاویه‌ای مناسب است.

روش مختصات (دترمینان)

روش مختصات یا دترمینان یک راه کاربردی برای محاسبه مساحت مثلث است که وقتی مختصات سه رأس مثلث در صفحه دکارتی (x₁,y₁)، (x₂,y₂) و (x₃,y₃) مشخص باشد، استفاده می‌شود. این روش به‌ویژه در هندسه تحلیلی بسیار مفید است، زیرا نیازی به دانستن قاعده، ارتفاع یا زوایا ندارد و تنها با استفاده از مختصات رئوس، مساحت را به‌دست می‌آورد.

فرمول این روش به‌صورت مساحت:  

مساحت = ½ × |(x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂))|

در این فرمول، مختصات رئوس در یک عبارت ریاضی ترکیب می‌شوند و مقدار مطلق نتیجه، تضمین می‌کند که مساحت همیشه مثبت باشد.

این روش برای مسائل هندسه تحلیلی کاربرد دارد.

دانلود کنید! محیط و مساحت اشکال هندسی به زبان ساده+ جزوه pdf

مساحت انواع خاص مثلث‌ها
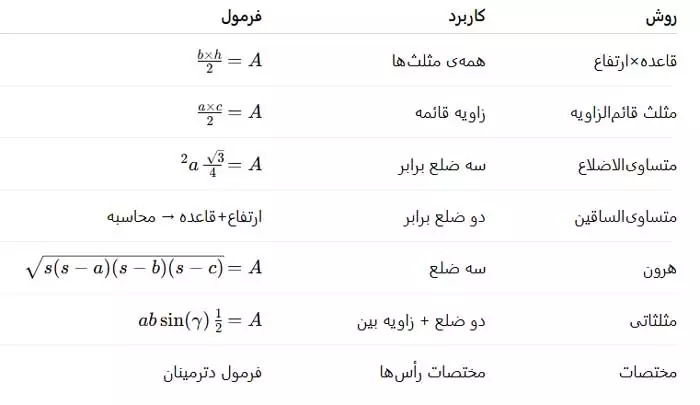
برخی مثلث‌ها فرمول‌های خاصی دارند که محاسبه را ساده‌تر می‌کنند:

• مثلث متساوی‌الاضلاع: اگر طول ضلع a باشد:

مساحت = (√3 ÷ 4) × a²

• مثلث قائم‌الزاویه: اضلاع مجاور زاویه قائمه به‌عنوان قاعده و ارتفاع عمل می‌کنند:

مساحت = ½ × ضلع اول × ضلع دوم

مثال: اضلاع مجاور زاویه قائمه 3 و 4 سانتی‌متر:

مساحت = ½ × 3 × 4 = 6 سانتی‌متر مربع

• مثلث متساوی‌الساقین: اگر قاعده b و طول ساق‌ها a باشد:

مساحت = (b × √(a² - (b² ÷ 4))) ÷ 2

• مثلث منفرجه: فرمول قاعده و ارتفاع همچنان معتبر است، اما ارتفاع ممکن است خارج از مثلث باشد. باید امتداد قاعده را در نظر گرفت.

کاربردهای مساحت مثلث در دنیای واقعی

محاسبه مساحت مثلث در موقعیت‌های عملی متعددی کاربرد دارد. در معماری، برای طراحی سقف‌های مثلثی یا سازه‌های پایدار از این محاسبات استفاده می‌شود. در کشاورزی، مساحت زمین‌های مثلثی‌شکل برای برنامه‌ریزی کاشت و برداشت محاسبه می‌شود.

 در طراحی صنعتی، مانند ساخت مبلمان یا دکوراسیون مثلثی، دانستن مساحت به تعیین مواد موردنیاز کمک می‌کند. همچنین، در هندسه پیشرفته، مثلث‌ها به‌عنوان پایه محاسبه مساحت چندضلعی‌های پیچیده استفاده می‌شوند.

یکبار برای همیشه یادشون بگیر: اشکال هندسی: آموزش کامل به زبان ساده و جزوه PDF

فیلم آموزش مساحت

نکات کلیدی برای یادگیری بهتر

برای تسلط بر محاسبه مساحت مثلث، دانش‌آموزان می‌توانند از این نکات استفاده کنند:

• تمرین منظم: حل مسائل متنوع با انواع مثلث‌ها به درک فرمول‌ها کمک می‌کند.
• رسم شکل: ترسیم مثلث و مشخص کردن قاعده، ارتفاع یا زوایا، فهم مسئله را آسان‌تر می‌کند.
• استفاده از ابزارها: خط‌کش، نقاله و ماشین‌حساب برای محاسبات دقیق مفید هستند.
• یادگیری فرمول‌های جایگزین: تسلط بر فرمول هرون و روش مثلثاتی برای مسائل پیچیده ضروری است.
• ارتباط با دنیای واقعی: مسائل را به موقعیت‌های عملی مانند محاسبه مساحت یک باغ مثلثی مرتبط کنید.

نتیجه‌گیری

محاسبه مساحت مثلث یکی از مهارت‌های کلیدی در هندسه است که با یادگیری دقیق، می‌تواند پایه‌ای برای حل مسائل پیچیده‌تر باشد. این مقاله با ارائه تعریف مثلث، انواع آن، فرمول‌های دقیق و مثال‌های کاربردی، تلاش کرد تا این موضوع را به‌صورت جامع و قابل‌فهم برای دانش‌آموزان توضیح دهد.

فوق کاربردی:  آموزش ریاضیات گسسته از صفر تا صد (و نکات و اصول)

از فرمول ساده قاعده و ارتفاع تا روش‌های پیشرفته مانند هرون و مختصات، تمام ابزارهای لازم برای تسلط بر این موضوع ارائه شده است. با تمرین مداوم و استفاده از منابع پیشنهادی، دانش‌آموزان می‌توانند این مهارت را به‌طور کامل یاد بگیرند و در مسائل واقعی به کار ببرند. حالا وقت آن است که خودتان چند مثلث رسم کنید و مساحت آن‌ها را محاسبه کنید!