آموزش مساحت استوانه 0 تا 100 و فرمول حجم+ PDF مثالها

استوانه، یکی از پرکاربردترین و آشناترین اشکال سهبعدی در اطراف ماست؛ از قوطیهای کنسرو گرفته تا لولههای آب و مخازن بزرگ نفتی. برای درک کامل این شکل هندسی، لازم است با مفاهیم پایهای آن، از جمله مساحت استوانه و حجم استوانه، آشنا شویم.
در این مقاله، قصد داریم به طور کامل و از صفر تا صد، تمامی جوانب مساحت و حجم استوانه را به زبانی ساده و قابل فهم آموزش دهیم. این راهنما برای هر کسی که میخواهد این مفاهیم را به طور کامل یاد بگیرد، از دانشآموزان گرفته تا دانشجویان، بسیار مفید است.
استوانه چیست؟
یک استوانه یک شکل سهبعدی است که از دو قاعده دایرهای شکل که با یک سطح منحنی به هم متصل شدهاند، تشکیل شده است.
فوق کاربردی: آموزش ریاضی از 0 تا دانشگاه با 30 درس+ PDF
ویژگیهای کلیدی استوانه:
- قاعدهها: دو دایره کاملاً یکسان (همنهشت) در بالا و پایین.
- شعاع (r) : شعاع هر یک از دایرههای قاعده.
- ارتفاع (h) : فاصله عمودی بین دو قاعده دایرهای.
- سطح جانبی: سطح منحنی که دو قاعده را به هم وصل میکند.

مساحت استوانه: درک کامل اجزا
برای محاسبه مساحت استوانه، باید دو بخش اصلی آن را در نظر بگیریم:
- مساحت قاعدهها: دو دایره همنهشت در بالا و پایین.
- مساحت سطح جانبی: سطح مستطیلشکلی که وقتی استوانه را باز میکنیم، نمایان میشود.
مساحت کل استوانه، برابر است با مجموع مساحت دو قاعده و مساحت سطح جانبی.
مساحت کل=مساحت دو قاعده+مساحت سطح جانبی
یکبار برای همیشه یادشون بگیر: اشکال هندسی: آموزش کامل به زبان ساده و جزوه PDF
فرمول مساحت استوانه (چگونه مساحت را به دست آوریم؟)
1. مساحت قاعدههاهمانطور که میدانید، هر استوانه دو قاعده دایرهای شکل دارد. فرمول مساحت دایره برابر با π×r2 است. از آنجا که دو قاعده داریم، مساحت هر دو قاعده به صورت زیر محاسبه میشود:
مساحت دو قاعده=2×(π×r<sup>2</sup>)
- π (پی): یک ثابت ریاضی است که تقریباً برابر با 3.14159 است. در اکثر محاسبات، استفاده از 3.14 یا کسر 22/7 کافی است.
- r: شعاع دایره قاعده.
اگر یک استوانه را از سطح منحنی آن برش داده و آن را باز کنید، به یک مستطیل تبدیل میشود.
- طول این مستطیل: برابر با محیط دایره قاعده است، یعنی 2πr .
- عرض این مستطیل: برابر با ارتفاع استوانه است، یعنی h .
بنابراین، مساحت این مستطیل (مساحت سطح جانبی) به صورت زیر محاسبه میشود:
مساحت سطح جانبی=طول×عرض=(2πr)×h
3. مساحت کل استوانهدانلود کنید! محیط و مساحت اشکال هندسی به زبان ساده+ جزوه pdf
حالا با جمع کردن مساحت قاعدهها و مساحت سطح جانبی، فرمول نهایی مساحت کل استوانه را به دست میآوریم:
مساحت کل=(مساحت دو قاعده)+(مساحت سطح جانبی)مساحت کل=(2πr<sup>2</sup>)+(2πrh)مساحت کل=2πr(r+h)فرمول نهایی برای مساحت کل استوانه
A=2πr(r+h)
- A: مساحت کل استوانه
- r: شعاع قاعده
- h: ارتفاع استوانه
حجم استوانه: درک مفهوم و فرمول
حجم یک جسم سهبعدی، مقدار فضایی است که آن جسم اشغال میکند. به بیان ساده، حجم استوانه، مقدار فضای داخلی آن است، مثلاً مقدار مایعی که میتوان در یک ظرف استوانهای شکل ریخت.
فرمول حجم استوانه بسیار ساده است:
حجم استوانه=مساحت قاعده×ارتفاع
از آنجا که مساحت قاعده یک دایره برابر با πr2 است، فرمول حجم استوانه به صورت زیر میشود:
V=(πr<sup>2</sup>)×h
- V: حجم استوانه
- r: شعاع قاعده
- h: ارتفاع استوانه
مثالهای کاربردی برای مساحت و حجم استوانه
در این بخش، با چند مثال متنوع، نحوه استفاده از این فرمولها را به طور کامل تمرین میکنیم.
مثال 1: محاسبه مساحت و حجم
یک استوانه با شعاع 3 سانتیمتر و ارتفاع 10 سانتیمتر داریم. مساحت کل و حجم آن را محاسبه کنید. (π≈3.14)
- محاسبه مساحت کل:
- A=2πr(r+h)
- A=2×3.14×3×(3+10)
- A=2×3.14×3×13
- A=6.28×39=244.92 سانتیمتر مربع.
- محاسبه حجم:
- V=πr2h
- V=3.14×32×10
- V=3.14×9×10
- V=3.14×90=282.6 سانتیمتر مکعب.
مثال 2: محاسبه شعاع با داشتن حجم و ارتفاع
حجم یک استوانه 180 سانتیمتر مکعب و ارتفاع آن 5 سانتیمتر است. شعاع قاعده آن چقدر است؟ (π≈3.14)
- پاسخ:
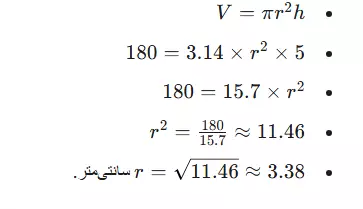
مثال 3: محاسبه ارتفاع با داشتن مساحت و شعاع
مساحت کل یک استوانه 150.72 سانتیمتر مربع و شعاع آن 2 سانتیمتر است. ارتفاع آن چقدر است؟ (π≈3.14)
- پاسخ:
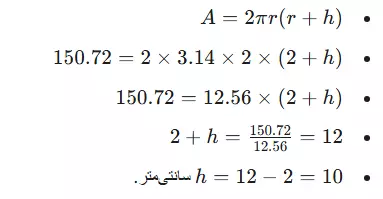
درصدگیری مهمترین مهارت ریاضی در زندگی! آموزش صفر تا صد و نکات (به زبان ساده)
سوالات متداول در مورد استوانه
تفاوت مساحت و حجم چیست؟- مساحت مقدار سطح یک جسم است (مثل رنگ مورد نیاز برای رنگآمیزی یک قوطی).
- حجم مقدار فضای داخلی یک جسم است (مثل مقدار آبی که در یک لیوان جا میشود).
- مساحت سطح جانبی برابر با محیط قاعده (دور تا دور دایره) ضرب در ارتفاع است.
- آیا مساحت استوانه میتواند منفی باشد؟
- خیر، مساحت و حجم همیشه مقادیری مثبت هستند، زیرا مربوط به ابعاد فیزیکی یک جسم هستند.
- واحد مساحت به صورت مربع (مثل m2 یا cm2) است.
- واحد حجم به صورت مکعب (مثل m3 یا cm3) است.
دانلود PDF
حجم: ۱۳ مگابایت
سطح: از صفر تا صد
نسخه آموزش داده شده: مناسب برای انواع استوانه
در این مقاله، به طور کامل با مفاهیم و فرمولهای مساحت و حجم استوانه آشنا شدید. آموختید که برای محاسبه مساحت کل، باید مساحت دو قاعده و مساحت سطح جانبی را با هم جمع کنید و برای محاسبه حجم، کافی است مساحت قاعده را در ارتفاع ضرب کنید. با درک این فرمولها و تمرین مثالهای متنوع، میتوانید به راحتی هر مسئلهای را در این زمینه حل کنید و درک عمیقتری از هندسه فضایی به دست آورید.







