راهنمای رسم نمودار Intercept در اکسل
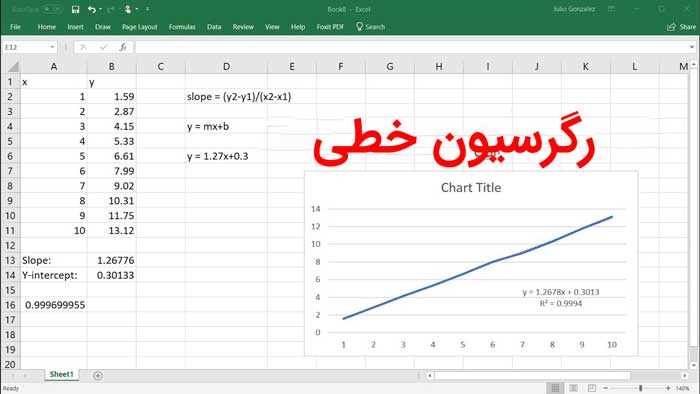
در تحقیقات علمی، محاسبه مقادیر پیش بینی شده الزامی است؛ زیرا در تحقیقات بازار یا علم داده، معمولا پیش بینی اهمیت بیشتری دارد. بنابراین، تابعIntercept هم در این جا اهمیت بیشتری پیدا می کند. تابع Intercept در اکسل یک تابع داخلی است که به عنوان یک تابع آماری طبقه بندی می شود. این تابع با استفاده از مقادیر x و y موجود، عرض از مبدا یا همان مکانی را محاسبه می کند که در آن یک خط، محور y را قطع می کند. با رسم خط بهترین برازش رگرسیون از طریق مقادیر x و y معلوم، نقطه Intercept را تعیین می کند.
ما در این مقاله، تابع Intercept در مایکروسافت اکسل را به همراه قاعده فرمول و کاربرد آن مورد بحث قرار خواهیم داد. علاوه بر این، یک خط رگرسیون را با استفاده از تابع Intercept ترسیم خواهیم کرد تا آن را به تصویر بکشیم.
دانلود فایل تمرین
این فایل تمرین را دانلود کنید تا بتوانید حین خواندن این مقاله از آن استفاده کنید:
مقدمه ای بر تابع Intercept در اکسل
هدف تابع:
بر اساس مقادیر معلومِ x و y ، تابع Intercept در اکسل مکانی را تعیین می کند که یک خط رگرسیون محور y را قطع می کند.
سینتکی تابع:
=Intercept (معلوم_y, معلوم_x)
توضیح آگومان ها:
| آرگومان | مورد نیاز/ اختیاری | توضیح |
| Y معلوم | نیاز است | مجموعه وابسته مشاهدات و داده ها |
| x معلوم | نیاز است | مجموعه مستقل مشاهدات و داده ها |
پارامتر بازگشتی:
تابع Intercept یک عدد به شما می دهد. در صورتی که آرگومان های مقادیر y معلوم و مقادیر xمعلوم دارای تعداد آیتم های متفاوتی باشند، خطای #N/A را برمی گرداند.
معادله
در یک مدل رگرسیون، تفسیر Intercept همیشه آن طور که به نظر می رسد ساده نیست. وقتی همه X=0 باشند، نقطه عرض از مبدا مقدار میانگین پیش بینی شده Y است.
بنابراین، اجازه بدهید تا با یک عامل پیش بینیکننده جدا مثل X، در یک معادله رگرسیونی شروع کنیم.
![]()
اگر X در مواقعی برابر 0 باشد، نقطه عرض از مبدا صرفا مقدار میانگین مورد انتظار Y در آن نقطه است که قابل توجه است. اگر X هیچ وقت برابر 0 نباشد، Intercept ارزش ذاتی ندارد. هر دوی این موارد اغلب در داده های دنیای واقعی رخ می دهند.
تابع Intercept از معادله زیر برای محاسبه فاصله خط رگرسیون خطی به کمک مجموعه ای از نقاط داده شده، استفاده می کند:
که در آن شیب، b و به صورت معادله زیر است:
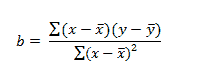
و مقادیر x و y میانگین نمونه مقادیر x و y معلوم هستند.
با این آموزش اکسل صفر تا صد اکسل، رو توی کمترین زمان ممکن یاد بگیر.بهترین پک آموزش اکسل در ایران همین الان خرید و دانلود کنید!
تابع Intercept: کاربرد اصلی و تحلیل رگرسیون
در این بخش، کاربرد اصلی تابع Intercept و تحلیل رگرسیون را نشان خواهیم داد.
کاربد اصلی تابع Intercept در اکسل
سناریوی زیر را در نظر بگیرید: شما یک مجموعه داده از برخی مقادیر مستقل (X) و برخی از مقادیر وابسته (Y) دارید. اما هیچ رابطه خطی بین X و Y مثل یک خط مستقیم وجود ندارد. بنابراین از تابع Intercept برای محاسبه مقدار یک متغیر وابسته، زمانی که متغیر مستقل صفر (0) باشد، استفاده می کنیم. فرمول زیر در این جا استفاده می شود:
=Intercept (B5:B13,C5:C13)
مرحله 1:
- تابع Intercept را در سلول C14 تایپ کنید.
- محدوده B5:B13 را برای متغیر وابسته Known_ys انتخاب کنید.
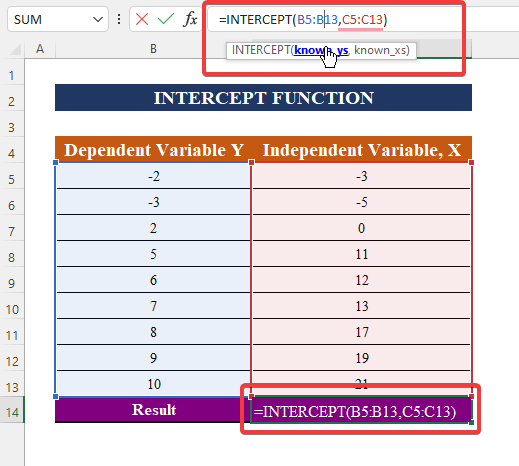
مرحله 2:
- محدوده C5:C13 را برای متغیر مستقل Known_xs انتخاب کنید.
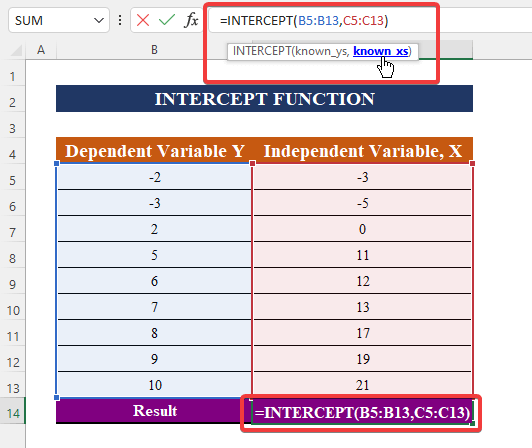
مرحله 3:
- Enter را فشار بدهید تا نتیجه را ببینید.
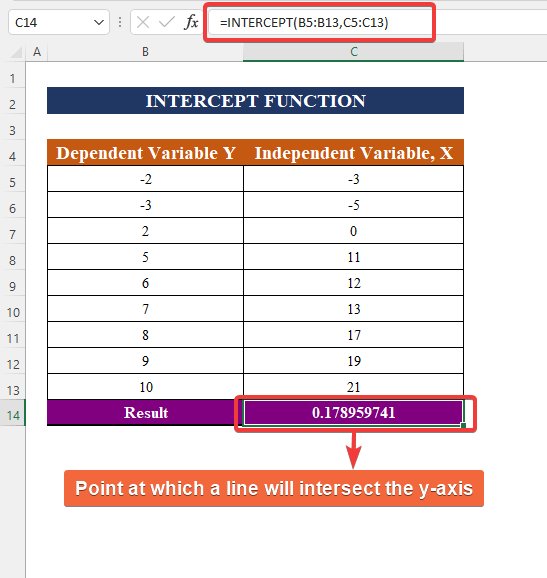
اگر اطلاعات بیشتری از رگرسیون می خواید: رگرسیون چیست؟ روش ساده اجرای آن در اکسل
تجزیه و تحلیل رگرسیون
در صفحه گسترده زیر، نقطه ای را پیدا می کنیم که خط رگرسیون خطی از طریق x معلوم و y معلوم از محور y عبور می کند.
به طور کلی، هدف یک مدل رگرسیون اینست که بفهمد عوامل پیش بینی کننده و پاسخ ها چه ربطی به هم دارند. اگر X هیچ وقت برابر 0 نباشد، Intercept هیچ فایده ای ندارد و چیزی در مورد رابطه X و Y به شما نمی گوید. اگر X هیچ وقت برابر 0 نیست؛ اما شما یک عرض از مبدا معنا دار می خواهید، X را در مرکز در نظر بگیرید.
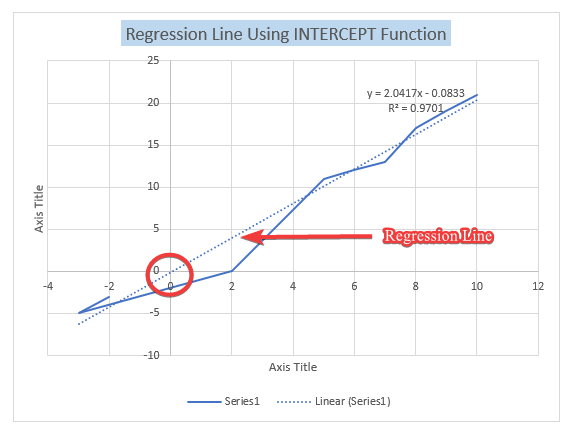
اگر X را مجددا عدد دهی کنید تا میانگین یا هر مقدار مرتبط دیگر مساوی 0 شود، عرض از مبدا حالا ربط دارد (خیلی راحت یک ثابت را از X حذف کنید). این مقدار متوسط Y در مقدار X مشخص شده است. از خط رگرسیون، متوجه شدیم که نقطه قطع از تجزیه و تحلیل رگرسیون با نقطه عرض از مبدا که با استفاده از تابع Intercept پیدا شده است ، مرتبط است.
حتما بخوانید: آموزش کامل رگرسیون خطی در اکسل
✍ چیز هایی که باید به خاطر بسپارید
✎ اعداد یا نام ها، آرایه ها یا مراجع حاوی اعداد باید به عنوان پارامتر استفاده شوند.
✎ متن، مقادیر منطقی و سلولهای خالی در آرایه یا آرگومان مرجع نادیده گرفته می شوند. با این حال، سلول های با مقدار صفر به حساب می آیند.
✎ تابع Intercept مقدار خطای #N/A را برمیگرداند؛ اگر y و x های معلوم دارای تعداد نقاط داده متفاوت باشند یا نقاط داده نداشته باشند.