ماتریس چیست؟ انواع آن و روش محاسبه

در این مقاله با تعریف ماتریس و ویژگی های آن آشنا می شوید و یاد می گیرید که چطور ابعاد ماتریس را پیدا کنید و عملیات اصلی را روی دو یا چند ماتریس انجام بدهید.
ماتریس چیست؟
ماتریس یک آرایش مستطیلی (یا آرایه) از اعداد است که به وسیله یک پرانتز محصور شده است. هر عدد در این آرایش، عنصری از ماتریس نامیده می شود. در این جا مثالی از ماتریس A آورده شده است که عناصر آن اعداد حقیقی هستند.
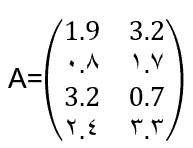
در زبان ریاضی بیشتر مرسوم است که یک ماتریس را محصور در براکت ببینیم تا پرانتز.
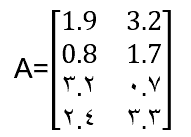
با این وجود معنا و ارزش مقداری چنین ماتریسی مثل ماتریسی است که با پرانتز محصور شده است. پس در واقع ماتریس یه جدول مستطیلی از اعداده که تو ریاضی و علوم مختلف برای مرتب کردن اطلاعات استفاده میشه، مثل یه صفحه شطرنج که به جاش عدد داره! مثلاً میتونه برای حل معادلات، تحلیل داده یا برنامهنویسی به کار بره.
انواع ماتریس شامل ماتریس مربعی (تعداد سطر و ستون برابره)، مستطیلی (سطر و ستون نابرابر)، صفر (همه عناصرش صفرن)، واحد (قطر اصلیش ۱ و بقیه صفرن) و معکوسپذیر (قابل معکوس کردن) میشه.
محاسبه ماتریس بسته به کارش فرق داره: برای جمع یا تفریق، دو ماتریس هماندازه رو عدد به عدد جمع یا کم میکنی. برای ضرب، تعداد ستونهای ماتریس اول باید با تعداد سطرهای دومی برابر باشه، بعد هر سطر ماتریس اول رو تو ستونهای دومی ضرب و جمع میکنی. مثلاً برای ضرب ماتریس ۲×۳ تو ۳×۲، هر درایه نتیجه از ضرب یه سطر تو یه ستون به دست میاد. سادهست، فقط نیاز به تمرین داره!
ماتریس ها در جبر خطی برای نمایش دستگاه معادلات خطی استفاده می شوند. نمونه ای از سه معادله خطی در یک دستگاه برای سه متغیر x، y و z آوردبه این صورت است:
x+2z=1.2
x+0.5y+z=−0.43
x+0.5y+0.5z=0.7
این سیستم معادلات به صورت ماتریسی به صورت زیر نمایش داده می شود:

یا حتی به طور خلاصه تر از ماتریس افزوده دستگاه استفاده کنید:

کاوش در ماتریس افزوده، (با استفاده از عملیات ماتریسی مثل جمع ، تفریق، ضرب و “عملیات سطری مقدماتی”) به ریاضیدان اجازه می دهد تا ویژگی های مهم دستگاه معادلات مثل این که آیا برای یک دستگاه راه حل منحصر به فردی وجود دارد یا خیر را تعیین کند. حتی می توان مشخص کرد که دستگاه بیش از یک راه حل، یا حتی هیچ راه حلی دارد یا خیر.
ابعاد ماتریس
شکل مستطیلی ماتریس امکان شناسایی آرایش (یا لیست) خطی عناصر ماتریس که به سطر و ستون معروف اند را فراهم می کند. ردیف ها در عرض صفحه نوشته می شوند، در حالی که ستون ها در طول آن نوشته می شوند. نمونه ای از یک ماتریس با چهار ردیف و دو ستون را می بینید:
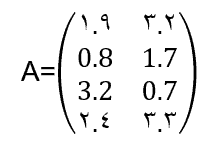
ردیف سوم ماتریس A به این صورت است:
(3.2 0.7)
و دومین ( و آخرین ) ستون A به این شکل است:
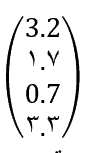
ابعاد یک ماتریس با تعداد سطر ها و ستون هایش مشخص می شود. ماتریسی با ردیف m و ستون n ماتریس m×n نامیده می شود. ماتریسA ( ماتریس تعریف شده در بالا ) یک ماتریس 4×2 است. توجه داشته باشید که تعداد عناصر یک ردیف ماتریس برابر با تعداد ستون های ماتریس و تعداد عناصر یک ستون ماتریس برابر با تعداد ردیف های ماتریس است.
عنصر یک ماتریس که در ردیف i و ستون j قرار دارد به عنوان درایه (i,j) ماتریس نامیده میشود.
حتما دانلود کنید: آموزش صفر تا صد زبان انگلیسی با 32 درس رایگان
ویژگی های ماتریس
ماتریس ها هنگامی که عملیات ماتریسی رویشان اعمال می شود؛ از چند ویژگی اساسی تبعیت می کنند. این ویژگی ها پایه و اساس جبر ماتریسی به حساب می آیند:
قانون شرکت پذیری
فرض کنید که A، B و C ماتریس هایی با ابعاد مساوی باشند . قانون شرکت پذیری برای عملیات جمع به این صورت است:
A+(B+C)=(A+B)+C
فرض کنید A یک ماتریس m×p و B یک ماتریس p×q باشد و C یک ماتریس q×n باشد. قانون شرکت پذیری برای ضرب ماتریس این گونه است:
A(BC)=(AB)C
قانون توزیع پذیری
فرض کنید که A یک ماتریس m×p باشد و B و C ماتریس های p×nباشند. در این حالت قانون توزیع پذیری این طور بیان می شود:
A(B+C)=AB+AC
همین طور اگر A یک ماتریس p×n باشد و B و C ماتریسهای m×p باشند، قانون توزیع پذیری به این صورت بیان می شود:
(B+C)A=BA+CA
ماتریس همانی
برای هر مقدار مشخصn ، یک ماتریس خاص n×n وجود دارد که ماتریس همانی نامیده و با I و گاهی اوقات In مشخص می شود که عناصر روی قطر آن 1 و بقیه عناصر 0 هستند.
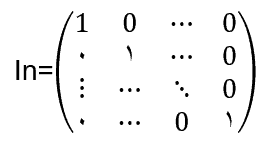
ماتریس همانی مشابه عدد حقیقی 1 عمل می کند ، یعنی از ضرب هر ماتریس m×n به نام A در ماتریس همانی خود ماتریس حاصل می شود:
AIn=A=ImA
عملیات ماتریسی
عملیات ماتریسی یک رویه (یا تابع) است که یک یا چند ماتریس را به عنوان ورودی می گیرد و یک ماتریس خروجی تولید می کند.
قوانین جمع ماتریس ها
فرض کنید A و B دو ماتریس m×n باشند. این دو ماتریس ممکن است برای تولید ماتریس سوم m×n یعنی ماتریس A+B، باید دو تای اولی با هم جمع شوند. ماتریس ها با رویه ای به نام جمع درایه ای با هم جمع بسته می شوند. جمع درایه ای به این معنا است که عنصر ( i,j) از A+B برابر است با مجموع عناصر (i,j) ماتریس های A وB. به طور مثال اگر ماتریس A در ردیف اول و ستون دومش دارای مقدار 2.0 و B در ردیف اول و ستون دومش دارای مقدار 6.0 باشد، مجموع آن ها مقدار 8.0 در ردیف اول و ستون دوم ماتریس A+B می شود. مثالی از جمع ماتریس انجام شده روی دو ماتریس 2×3 به این صورت است:
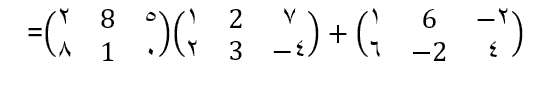
برای این که بتوان دو ماتریس را با هم جمع کرد، ابعاد دو ماتریس باید با هم برابر باشد.
قوانین تفریق ماتریسی
مجددا فرض کنید که A و B دو ماتریس m×n باشند . تفریق ماتریس زمانی روی دو ماتریس انجام می شود که ماتریس حاصل هم به صورت m×n تولید شود. ماتریس تفاضل با A−B نشان داده می شود. تفریق ماتریسی با استفاده از روشی به نام تفریق درایه ای انجام می شود، که در آن عنصر (i,j) ماتریس A−B، از تفریق عنصر (i,j) ماتریس B از عنصر (i,j) ماتریس A حاصل شود . نمونهای از تفریق ماتریسی که روی دو ماتریس 3×2 انجام شده است را با هم می بینیم:
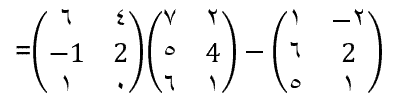
همانند ماتریس جمع، در ماتریس تفریق هم ابعاد دو ماتریس باید با هم یکی باشند.
در کنار این مطلب بخوانید: واریانس چیست؟ فرمول محاسبه آن






نفهمیدم
پاسخویدیو رو ببینید، هر چیزی که از ماتریس نیاز دارید رو توی 15 دقیقه کامل یاد می گیرید