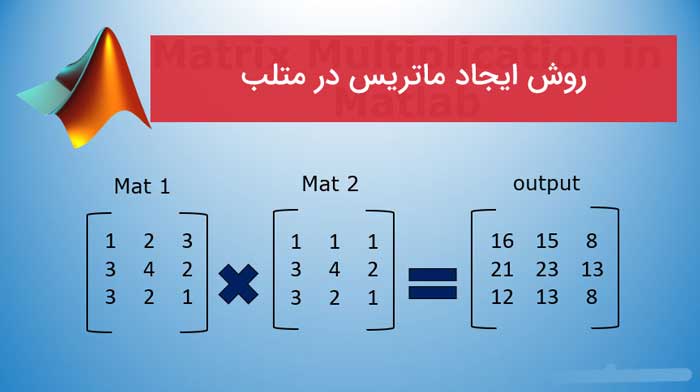
ماتریس ترانهاده در متلب (آموزش کامل)
در این مقاله ، ما با ماتریس ترانهاده Matlab آشنا خواهیم شد. اگر ردیف های ماتریس خروجی برابر ستون های ورودی و ستون های ماتریس خروجی برابر ردیف های ماتریس ورودی باشند ، ماتریس خروجی “ترانهاده ماتریس” نامیده می شود. این ” T نشان دهنده انتقال ماتریس است. بیایید در نظر بگیریم که دو ماتریس وجود دارد یکی ماتریس ورودی “”Iو دوم ماتریس خروجی “” O است. تعدادی از ردیف های ماتریس ورودی “” Irow هستند. تعداد ستون های ماتریس ورودی “” Idol و تعداد ردیف های ماتریس خروجی “” Orow است. تعداد ستون ها در ماتریس خروجی “” Ocol است و سپس انتقال ماتریس دو شرط را برآورده می کند:
Icol = Orow و Irow = Ocol. (ردیف های ماتریس ورودی = ستون ماتریس خروجی و ستون های ماتریس ورودی = ردیف های ماتریس خروجی)
چطور میتوانیم در متلب ماتریس ترانهاده انجام پیاده کنیم؟
برای پیدا کردن ترانهاده یک ماتریس در Matlab دو روش وجود دارد:
- با استفاده از عملگر (operator)
- با استفاده از فرمان (Command)
1- با استفاده از عملگر (operator)
در این روش ، از دستور ‘transpose’ برای یافتن ترانزیست ماتریس استفاده می شود. این روش در مقایسه با روش قبلی از پیچیدگی کمتری برخوردار است و اجرای آن آسان است. و در زمان اجرا خطاهای کمتری وجود دارد. در این روش ، از عملگر نقطه برای یافتن ترانهاده ماتریس (. ’) استفاده می شود. این یکی از ساده ترین و ساده ترین روش ها برای محاسبه ی ترانهاده است. تنها محدودیت این روش این است که احتمال سینتکس ارور به دلیل اپراتور زیاد است.
Syntax:
Output matrix=input matrix . ’
مراحل:
- ماتریس ورودی را با استفاده از ماتریس مربع بپذیرید Input = [ 23 , 32 , 11 ; 22 3 2 ; 16 39 21 ; 32 4 1 ])
- عملگر را روی ماتریس ورودی اعمال کنید (ماتریس خروجی = ماتریس ورودی. ‘) ( output matrix=input matrix.’)
- ماتریس خروجی را نمایش دهید.
2. با استفاده از Command
در این روش ، از دستور ” transpose برای یافتن ترانهاده ماتریس استفاده می شود. این روش در مقایسه با روش قبلی از پیچیدگی کمتری برخوردار است و اجرای آن آسان است. و در زمان اجرا خطاهای کمتری وجود دارد.
Syntax:
Output matrix=transpose (input matrix)
مراحل:
- ماتریس ورودی را با استفاده از ماتریس مربع بپذیرید Input = [ 23 , 32 , 11 ; 22 3 2 ; 16 39 21 ; 32 4 1 ])
- اعمال دستور روی ماتریس ورودی (ماتریس خروجی = ترانهاده (ماتریس ورودی))
- نمایش ماتریس خروجی
مثال برای ترانهاده ماتریس در Matlab
در زیر مثالهایی برای اجرای ماتریس Matlab آورده شده است:
مثال شماره ۱:
اجازه دهید ماتریس ورودی را mat1 در نظر بگیریم.
Code:
mat1 =
23 32 11
22 3 2
16 39 21
32 4 1
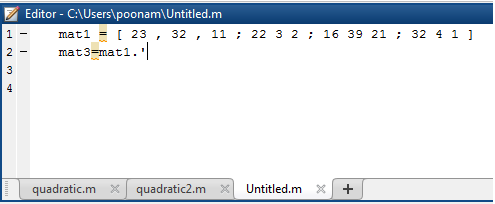
جدول زیر کد Matlab را برای مثال 1 با استفاده از عملگر نشان می دهد.
| ویرایشگر Matlab | پنجره فرمان (خروجی) |
|
mat1 = [ 23 , 32 , 11 ; 22 3 2 ; 16 39 21 ; 32 4 1 ] mat3 = mat1 . ‘ |
mat1 =
23 32 11 22 3 2 16 39 21 32 4 1 mat3 = 23 22 16 32 32 3 39 4 11 2 21 1 |
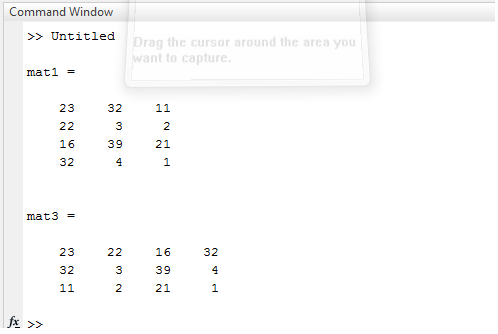
خروجی:

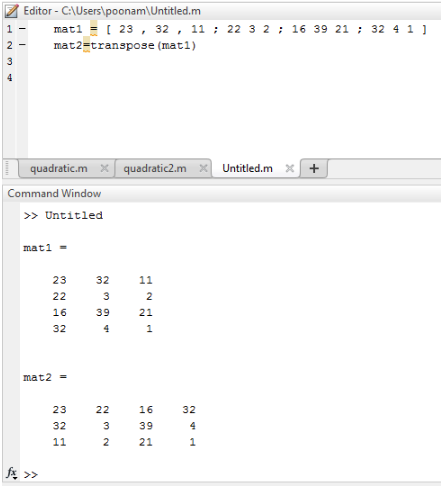
جدول زیر کد Matlab را برای مثال 1 با استفاده از دستور ترانهاده نشان می دهد:
| ویرایشگر Matlab | پنجره فرمان (خروجی) |
|
mat1 = [ 23 , 32 , 11 ; 22 3 2 ; 16 39 21 ; 32 4 1 ] mat2=transpose(mat1) |
mat1 =
23 32 11 22 3 2 16 39 21 32 4 1 mat2 = 23 22 16 32 32 3 39 4 11 2 21 1 |
مثال شماره 2
اجازه دهید فرض کنیم ماتریس ورودی از نظر دستور جادویی mat1 باشد.
mat1 =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
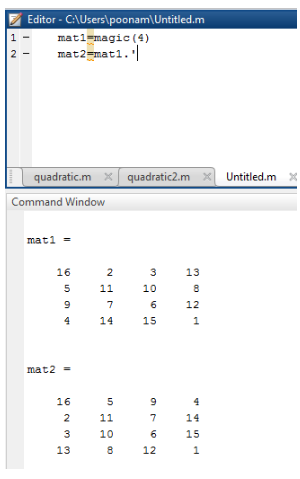
جدول زیر کد Matlab را به عنوان مثال 1 با استفاده از یک عملگر ترانهاده نشان می دهد.
| ویرایشگر Matlab | پنجره فرمان (خروجی) |
|
mat1 = magic(4) mat2 = mat1.’ |
mat1 =
16 2 3 13 5 11 10 8 9 7 6 12 4 14 15 1 mat2 = 16 5 9 4 2 11 7 14 3 10 6 15 13 8 12 1 |
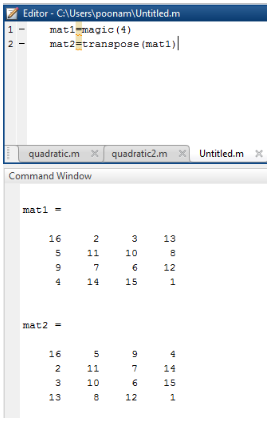
جدول زیر کد Matlab را برای مثال 2 با استفاده از دستور ترانهاده نشان می دهد.
| ویرایشگر Matlab | پنجره فرمان (خروجی) |
|
mat1 = magic ( 4 )%no 4 represents no of rows and columns% mat2=transpose(mat1) |
mat1 =
16 2 3 13 5 11 10 8 9 7 6 12 4 14 15 1 mat2 = 16 5 9 4 2 11 7 14 3 10 6 15 13 8 12 1 |
مثال شماره 3
حال یک ماتریس ورودی را با اعداد مختلط در نظر بگیرید.
mat1 =
1.0000 – 3.0000 i 4.0000 + 4.0000 i 8.0000 + 0.0000 i 2.0000 – 5.0000 i
5.0000 + 0.0000 i 3.0000 + 0.0000 i 6.0000 + 8.0000 i 4.0000 + 4.0000 i
0.0000 + 1.0000 i 7.0000 + 8.0000 i 9.0000 + 9.0000 i 10.0000 + 0.0000 i
| ویرایشگر Matlab | پنجره فرمان (خروجی) |
|
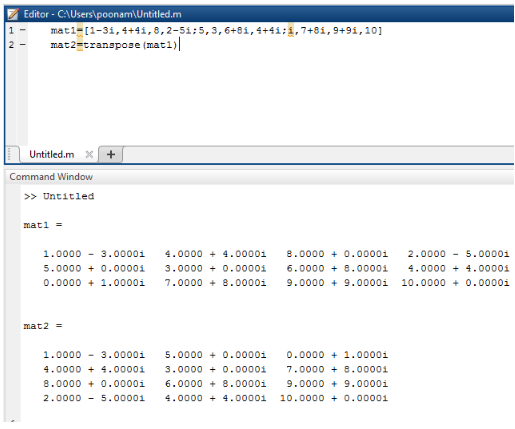
mat1 = [ 1 – 3 i , 4 + 4 i , 8 , 2 – 5 i ; 5 , 3 , 6 + 8 i , 4 + 4 i ; i , 7 + 8 i , 9 + 9 i , 10] mat2=mat1.’ |
mat1 =
1.0000 – 3.0000i 4.0000 + 4.0000i 8.0000 + 0.0000i 2.0000 – 5.0000i 5.0000 + 0.0000i 3.0000 + 0.0000i 6.0000 + 8.0000i 4.0000 + 4.0000i 0.0000 + 1.0000i 7.0000 + 8.0000i 9.0000 + 9.0000i 10.0000 + 0.0000i mat2 = 1.0000 – 3.0000i 5.0000 + 0.0000i 0.0000 + 1.0000i 4.0000 + 4.0000i 3.0000 + 0.0000i 7.0000 + 8.0000i 8.0000 + 0.0000i 6.0000 + 8.0000i 9.0000 + 9.0000i 2.0000 – 5.0000i 4.0000 + 4.0000i 10.0000 + 0.0000i |

| ویرایشگر Matlab | پنجره فرمان (خروجی) |
|
mat1=[1-3i,4+4i,8,2-5i;5,3,6+8i,4+4i;i,7+8i,9+9i,10] mat2=transpose(mat1) |
mat1 =
1.0000 – 3.0000i 4.0000 + 4.0000i 8.0000 + 0.0000i 2.0000 – 5.0000i 5.0000 + 0.0000i 3.0000 + 0.0000i 6.0000 + 8.0000i 4.0000 + 4.0000i 0.0000 + 1.0000i 7.0000 + 8.0000i 9.0000 + 9.0000i 10.0000 + 0.0000i mat2 = 1.0000 – 3.0000i 5.0000 + 0.0000i 0.0000 + 1.0000i 4.0000 + 4.0000i 3.0000 + 0.0000i 7.0000 + 8.0000i 8.0000 + 0.0000i 6.0000 + 8.0000i 9.0000 + 9.0000i 2.0000 – 5.0000i 4.0000 + 4.0000i 10.0000 + 0.0000i |
نتیجه
ترانهاده ماتریس یکی از اصطلاحات مهم مورد استفاده در دستکاری های ماتریس است. در این بخش ما دیده ایم که چگونه می توان با استفاده از دو روش ترانهادهماتریس را پیدا کرد یکی با استفاده از عملگر و دیگری با استفاده از دستور transpose. در کنار روشهای مختلف ، ما ماتریسهای مختلفی را به عنوان ورودی برای بررسی سیستم مشاهده کرده ایم (اعداد واقعی ، اعداد تصادفی و اعداد مختلط).