حل معادله در متلب با انواع روشها (در سریعترین زمان)

معادلات چند جمله ای از معروفترین انواع معادلات در ریاضی هستند. دانستن نحوه حل آنها یک چیز است اما در واقع حل عملی آنها چیز دیگری است. روش های زیادی برای حل این معادلات وجود دارد اما اگر هدفتان بیشتر حل معادله باشد تا راه حل معادله می توانید با استفاده از متلب در زمان خود صرفه جویی کنید.

نکته: روش های زیر کمک می کند تا معادلات چند جمله ای را به سرعت حل کنید اما نحوه حل دستی آنها را نشان نمی دهند. با استفاده از این روش ها به راحتی می توانید سریعترین نتیجه بگیرید.

حل معادلات پایه ریاضی با تابع solve در متلب

از تابع solve برای حل معادلات ریاضی در متلب استفاده می شود. در ساده ترین حالت آن، تابع solve معادله ریاضی را بین علامت های نقل قول ها به عنوان آرگومان ورودی دریافت می کند.

برای مثال معادله زیر را در نظر بگیرید، می خواهیم مقدار x را در آن به دست آوریم:

solve(‘x-5=0’)

خروجی

ans =

5

می توانید تابع را به صورت زیر نیز فراخوانی کنید:

y = solve(‘x-5 = 0’)

خروجی

y =

5

اگر سمت راست معادله را وارد نکنید:-

solve(‘x-5’)

خروجی

ans =

5

اگر معادله شامل چند متغیر یا نماد باشد، متلب به طور پیشفرض آن را براساس x حل می کند. با این حال تابع solve فرم دیگری نیز دارد:

solve(معادله, متغیر)

در این فرم می توانید متغیر مورد نظر در معادله را مشخص کنید.

به عنوان مثال برای حل معادله v – u – 3t² = 0 براساس متغیر v باید به شکل زیر نوشته شود:

solve(‘v-u-3*t^2=0’, ‘v’)

متلب دستور بالا را اجرا کرده و نتیجه زیر را برمی گرداند:

ans =

3*t^2 + u

حل معادلات درجه دو با تابع solve در متلب

تابع solve برای حل معادلات مرتبه بالاتر به خصوص معادلات درجه دوم نیز استفاده می شود.

فرم کلی معادله درجه دوم به شکل زیر است:

به صورتی که،

معادلات درجه دوم به فرم های زیر نیز نوشته می شوند:

تابع solve ریشه های معادله را در یک آرایه برمیگرداند.

معادله درجه دو x² -7x +12 = 0 را در نظر بگیرید. کد زیر را تایپ کنید:

eq = ‘x^2 -7*x + 12 = 0’;

s = solve(eq);

disp(‘The first root is: ‘), disp(s(1));

disp(‘The second root is: ‘), disp(s(2));

نتیجه زیر برگردانده می شود: –

The first root is:

3

The second root is:

4

حل معادلات درجه بالاتر با تابع solve در متلب

تابع solve می تواند معادلات مرتبه های بالاتر را حل کند. به عنوان مثال معادله درجه سه زیرا را در نظر بگیرید:

تابع solve به شکل زیر نوشته می شود:

solve(‘(x-3)^2*(x-7)=0’)

متلب دستور بالا را اجرا کرده و نتیجه زیر را برمیگرداند:

ans =

3

3

7

برای معادلات با درجه های بالاتر ریشه ها اعشار طولانی دارند. برای کوتاه کردن تعداد اعشار می توانید از نوع double استفاده کنید. معادله مرتبه چهار زیر را در نظر بگیرید:

x⁴ − 7x³ + 3x² − 5x + 9 = 0

کد زیر را در متلب تایپ کنید:

eq = ‘x^4 – 7*x^3 + 3*x^2 – 5*x + 9 = 0’;

s = solve(eq);

disp(‘The first root is: ‘), disp(s(1));

disp(‘The second root is: ‘), disp(s(2));

disp(‘The third root is: ‘), disp(s(3));

disp(‘The fourth root is: ‘), disp(s(4));

% double استفاده از نوع

disp(‘Numeric value of first root’), disp(double(s(1)));

disp(‘Numeric value of second root’), disp(double(s(2)));

disp(‘Numeric value of third root’), disp(double(s(3)));

disp(‘Numeric value of fourth root’), disp(double(s(4)));

نتیجه زیر را برمیگرداند،

The first root is:

6.630396332390718431485053218985

The second root is:

1.0597804633025896291682772499885

The third root is:

– 0.34508839784665403032666523448675 – 1.0778362954630176596831109269793*i

The fourth root is:

– 0.34508839784665403032666523448675 + 1.0778362954630176596831109269793*i

Numeric value of first root

6.6304

Numeric value of second root

1.0598

Numeric value of third root

-0.3451 – 1.0778i

Numeric value of fourth root

-0.3451 + 1.0778i

نکته: توجه داشته باشید که دو ریشه آخر اعداد مختلط هستند.

حل دستگاه معادلات با تابع solve در متلب

تابع solve برای حل دستگاه های معادلات با بیش از یک متغیر نیز استفاده شود. این را با یک مثال ساده نشان می دهیم.

معادلات زیر را در نظر بگیرید:

5x + 9y = 5

3x – 6y = 4

برای به دست آوردن حل آن، کد زیر را در متلب تایپ کنید،

s = solve(‘5*x + 9*y = 5′,’3*x – 6*y = 4’);

s.x

s.y

خروجی

ans =

22/19

ans =

-5/57

به همین ترتیب می توانید دستگاه های معادلات خطی بزرگتر مانند مثال زیر را نیز حل کنید.

x + 3y -2z = 5

3x + 5y + 6z = 7

2x + 4y + 3z = 8

حل معادلات درجه دو با استفاده از تابع roots

همانطور که گفتیم فرم کلی معادله درجه دو به شکل زیر است:

در ادامه نحوه حل معادله زیر را با استفاده از تابع roots توضیح می دهیم.

کد زیر را در متلب وارد کنید:

roots([1 -3 2])

متلب ریشه های معادله چند جمله ای را برمیگرداند:

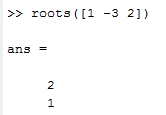
برای معادله زیر،

کد زیر را باید در متلب وارد کنید:

roots([1 0 -4])

خروجی:

حل معادلات درجه سه با استفاده از تابع roots

معادله زیر را در نظر بگیرید:

کد متلب آن در مقایسه با مثال قبلی تفاوت زیادی ندارد. تنها تفاوت در اینجا اضافه شدن ضریب درجه سوم غیر صفر است.

roots([1 6 0 -20])

نکته: دقت داشته باشید که 0 را بین 6 تا -20 وارد کنید زیرا ضریب جمله مرتبه اول معادله برابر با صفر است.

نتیجه زیر را برمیگرداند:

حل معادلات درجه چهار با استفاده از تابع roots

معادله چند جمله ای درجه چهار زیر را در نظر بگیرید:

کد متلب آن،

roots([1 2 -6*sqrt(10) +1])

نتیجه زیر را برمیگرداند:

برای معادلات با درجه های بالاتر تعداد ضریب ها بیشتر می شود. فقط باید ترتیب وارد کردن ضریب ها در کد رعایت شود زیرا روی نتیجه تأثیر می گذارد. همیشه به یاد داشته باشید که 0 برای نشان دادن ضریبی است که در معادله وجود ندارد.

آموزش کامل برنامه نویسی در متلب (22 جلسه رایگان به زبان فارسی)

توابع expand و collect در متلب

توابع expand و collect به ترتیب برای گسترش و جمع آوری معادله در متلب به کار می روند. مثال زیر این مفاهیم را بهتر نشان خواهد داد.

زمانیکه با توابع نمادین کار می کنید باید متغیرهای نمادین را تعریف کنید. متغیر نمادین یا سمبلیک در متلب یعنی اینکه عدد خاصی به آن متغیر نسبت نمی دهیم و تنها با نماد آن کار می کنیم همانطور که بسیاری از معادلات ریاضی به همین ترتیب حل می شوند. دو نماد x و y رایجترین نمادها هستند.

در متلب از دستور syms برای تعریف متغیر نمادین استفاده می شود.

syms x %symbolic variable x

syms y %symbolic variable y

% expanding equations

expand((x-5)*(x+9))

expand((x+2)*(x-3)*(x-5)*(x+7))

expand(sin(2*x))

expand(cos(x+y))

% collecting equations

collect(x^3 *(x-7))

collect(x^4*(x-3)*(x-5))

نتیجه زیر را برمیگرداند:

ans =

x^2 + 4*x – 45

ans =

x^4 + x^3 – 43*x^2 + 23*x + 210

ans =

2*cos(x)*sin(x)

ans =

cos(x)*cos(y) – sin(x)*sin(y)

ans =

x^4 – 7*x^3

ans =

x^6 – 8*x^5 + 15*x^4

تعریف تابع در متلب (ساده ترین روش)

فاکتورگیری و ساده سازی عبارت های جبری در متلب

تابع factor یک عبارت را در معادله فاکتورگیری می کند و تابع simplify یک عبارت را ساده می کند. در مثال زیر این مفاهیم بهتر نشان داده شده است:

syms x

syms y

factor(x^3 – y^3)

factor([x^2-y^2,x^3+y^3])

simplify((x^4-16)/(x^2-4))

نتیجه زیر را برمیگرداند:

ans =

(x – y)*(x^2 + x*y + y^2)

ans =

[ (x – y)*(x + y), (x + y)*(x^2 – x*y + y^2)]

ans =

x^2 + 4

آموزش مشتق در متلب (به زبان ساده)