انتگرال در متلب (آموزش به زبان ساده)

در این آموزش به زبانی کاملا ساده، انتگرال در متلب را یاد می گیرید، به صورت گام به گام و با مثال های کاربردی. با سریع آسان همراه باشید.
اگر f یک عبارت نمادین باشد، پس:
int (f)
تلاش می کند تا عبارت نمادین دیگر F را پیدا کند به طوری که diff (F) = f. یعنی int (f) انتگرال نامعین یا ضد مشتق f را برمی گرداند. مشابه مشتق گیری،
int(f,v)
از شی نمادین v به عنوان متغیر انتگرال به جای متغیر تعیین شده توسط symvar استفاده می کند. در جدول زیر نحوه کار int را مشاهده می کنید:
| دستور متلب | عملیات ریاضی |
|---|---|
|
int(x^n) یا int(x^n,x) |
|
|
int(sin(2*x), 0, pi/2) یا int(sin(2*x), x, 0, pi/2) |
|
|
g = cos(a*t + b) int(g) یا int(g, t) |
g = cos(at + b) |
|
int(besselj(1, z)) یا int(besselj(1, z), z) |
انتگرال برخلاف مشتق گیری کار پیچیده تری است و موارد سخت بیشتری در محاسبه انتگرال وجود دارد:
- ضد مشتق F ممكنه در فرم بسته وجود نداشته باشد.
- ضد مشتق ممکنه یک تابع نا شناخته تعریف کند.
- ضد مشتق ممکنه وجود داشته باشد اما نرم افزار نمی تواند آن را پیدا کند.
- نرم افزارهای کامپیوترهای بزرگتر می تواند انتگرال را در پیدا کند اما مشکل زمان طولانی یا حافظه کم وجود دارد.
با این وجود در بسیاری از موارد متلب می تواند انتگرال را با موفقیت انجام دهد. به عنوان مثال متغیرهایی زیر را در نظر بگیرید:
syms a b theta x y n u z
جدول زیر چند انتگرال حاوی این متغیرها را نشان می دهد:
| f | int(f) |
|---|---|
|
syms x n f = x^n; |
int(f) ans = piecewise(n == -1, log(x), n ~= -1,… x^(n + 1)/(n + 1)) |
|
syms y f = y^(-1); |
int(f) ans = log(y) |
|
syms x n f = n^x; |
int(f) ans = n^x/log(n) |
|
syms a b theta f = sin(a*theta+b); |
int(f) ans = -cos(b + a*theta)/a |
|
syms u f = 1/(1+u^2); |
int(f) ans = atan(u) |
|
syms x f = exp(-x^2); |
int(f) ans = (pi^(1/2)*erf(x))/2 |
مثال آخر exp(-x^2) را ببینید، هیچ فرمولی انتگرال برای عبارات استاندارد حسابی مانند توابع مثلثاتی و نمایی وجود ندارد. در این مورد متلب تابع خطا erf را برمی گرداند.
اگر متلب نتواند پاسخی برای انتگرال یک تابع f پیدا کند، فقط int(f) را برمی گرداند.
امکان محاسبه انتگرال معین نیز وجود دارد:
int(f, a, b)
int(f, v, a, b)
در اینجا چند مثال آورده شده است.
| f | a, b |
int(f, a, b) |
|---|---|---|
|
syms x f = x^7; |
a = 0; b = 1; |
int(f, a, b) ans = 1/8 |
|
syms x f = 1/x; |
a = 1; b = 2; |
int(f, a, b) ans = log(2) |
|
syms x f = log(x)*sqrt(x); |
a = 0; b = 1; |
int(f, a, b) ans = -4/9 |
|
syms x f = exp(-x^2); |
a = 0; b = inf; |
int(f, a, b) ans = pi^(1/2)/2 |
|
syms z f = besselj(1,z)^2; |
a = 0; b = 1; |
int(f, a, b) ans = hypergeom([3/2, 3/2],… [2, 5/2, 3], -1)/12 |
برای مثال تابع بسل (besselj) می تواند تقریب عددی را با مقدار انتگرال با استفاده از تابع double محاسبه کرد.
دستور زیر
syms z
a = int(besselj(1,z)^2,0,1)
خرروجی زیر را بر می گراند:
a =
hypergeom([3/2, 3/2], [2, 5/2, 3], -1)/12
و دستور زیر
a = double(a)
خرروجی زیر را بر می گراند:
a =
0.0717
انتگرال با پارامترهای حقیقی
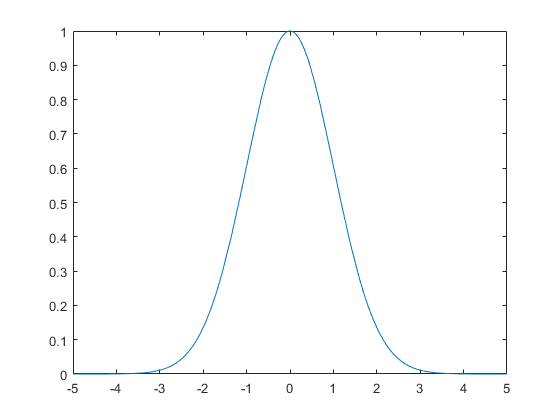
یکی از نکات ظریف “مقدار” پارامترهای مختلف است. برای مثال اگر a عدد حقیقی مثبت باشد، عبارت
e−ax2
مثبت است و منحنی آن به شکل یک زنگوله است که برای مقادیر x رو به ±∞ متمایل به 0 است. نمونه ای از این منحنی برای a = 1/2 در ادامه آورده شده است.
syms x
a = sym(1/2);
f = exp(-a*x^2);
fplot(f)
با این حال اگر بخواهید انتگرال زیر را محاسبه کنید
و a نیز بدون مقدار باشد، در این صورت متلب فرض می کند که a یک عدد مختلط است و در نتیجه یک پاسخ چند قسمتی براساس آرگومان a برمی گرداند. اگر می خواهید a یک عدد حقیقی مثبت باشد از assume برای تعیین یک فرض برای a استفاده کنید:
syms a
assume(a > 0)
حالا می توانید انتگرال قبلی را با استفاده از دستورات زیر محاسبه کنید:
syms x
f = exp(-a*x^2);
int(f, x, -inf, inf)
نتیجه زیر را نشان می دهد:
ans =
pi^(1/2)/a^(1/2)
کجا و به چه دلیل باید از نرم افزار متلب استفاده کنیم یا نکنیم؟
انتگرال با پارامترهای پیچیده
برای محاسبه انتگرال برای مقادیر پیچیده a، کد زیر را وارد کنید:
syms a x
f = 1/(a^2 + x^2);
F = int(f, x, -inf, inf)
از syms برای پاکسازی همه مفروضات متغیرها استفاده می شود.
دستورات قبلی خروجی های پیچیده را تولید می کنند.
F =
(pi*signIm(1i/a))/a
تابع signIm به صورت زیر تعریف می شود:
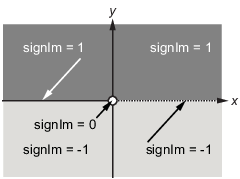
برای ارزیابی F در a = 1 + i دستورات زیر را وارد کنید:
g = subs(F, 1 + i)
g =
pi*(1/2 – 1i/2)
double(g)
ans =
1.5708 – 1.5708i
انتگرال عددی با دقت بالا
انتگرال عددی با دقت بالا با تابع vpaintegral از ابزار ریاضی متلب پیاده سازی می شود. vpaintegral در مقایسه با تابع integral با دقت مضاعف از دقت متغیر استفاده می کند.
انتگرال besseli(5,25*u).*exp(-u*25)را با استفاده از هر دو تابع integral و vpaintegral را محاسبه می کنیم. تابع integral مقدار NaN را برمی گرداند و یک پیغام خطا نشان می دهد در حالیکه vpaintegral نتیجه درست را برمی گرداند.
syms u
f = besseli(5,25*x).*exp(-x*25);
fun = @(u)besseli(5,25*u).*exp(-u*25);
usingIntegral = integral(fun, 0, 30)
usingVpaintegral = vpaintegral(f, 0, 30)
Warning: Infinite or Not-a-Number value encountered.
usingIntegral =
NaN
usingVpaintegral =
0.688424
حتما دانلود کنید: آموزش کامل برنامه نویسی در متلب (22 جلسه رایگان به زبان فارسی)