روش گوس سایدل در متلب از صفر تا صد و نکات کاربردی

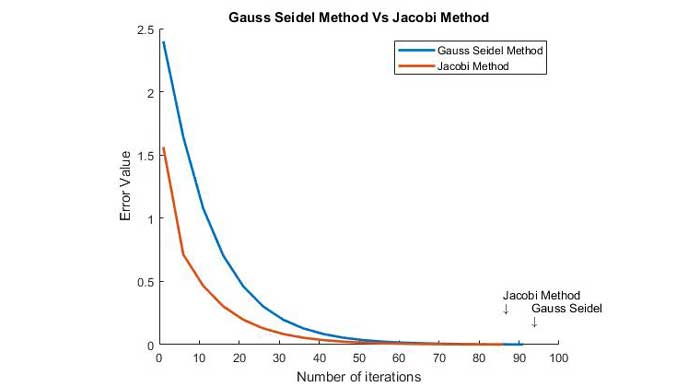
روش گوس سایدل یا گاوس سایدل (Gauss-Seidel) یکی از انواع روشهای تکراری (Iterative) رایج برای حل دستگاه معادلات خطی جبری است. این روش را می توان روی هر ماتریس همگرا با عناصر غیر صفر بر روی مورب ها اعمال کرد. نام روش گوس سایدل از نام دو ریاضیدان آلمانی به نام های کارل فردریش گاوس (Carl Friedrich Gauss) و فیلیپ لودویگ فون سایدل (Philipp Ludwig von Seidel) گرفته شده است.

در واقع گوس سایدل روش پیشرفته تر و نسخه ارتقا یافته روش گوس ژاکوبی (Gauss Jacobi) محسوب می شود. در این روش هم درست مثل هر روش تکراری دیگری، معادلات داده شده به صورت تقریبی حل می شوند و تا زمان حصول میزان دقت مطلوب، تکرار انجام می شود.

حتما بخوانید: دانلود رایگان ۱۳ فیلم کاربردی آموزش شبکه عصبی در متلب

در این مطلب ما قصد داریم یک کد برنامه به روش گوس سایدل در متلب (MATLAB) بنویسیم و در کنار آن پیشینه نظری این روش را مورد بررسی قرار بدهیم و در نهایت، نتیجه برنامه متلب را با یک مثال عددی تجزیه و تحلیل کنیم.

نظریه روش گوس سایدل

اول از همه بهتر است نگاه مختصری به پیشینه نظری/ ریاضی روش گوس سایدل داشته باشیم. ماتریس ها، تکرارها و روشی که در ادامه به آن اشاره می کنیم دستورالعمل های پایه و اولیه برای نوشتن کد برنامه برای روش گوس سایدل در متلب هستند.

دستگاه معادلات خطی زیر را در نظر بگیرید:

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + a₁₄x₄ + a₁₅x₅ + a₁₆x_{6 …….} + a_1nx_n = b₁
a₂₁x₁ + a₂₂x₂ + a₂₃x₃ + a₂₄x₄ + a₂₅x₅ + a₂₆x_{6 …….} + a_2nx_n = b₂
a₃₁x₁ + a₃₂x₂ + a₃₃x₃ + a₃₄x₄ + a₃₅x₅ + a₃₆x_{6 …….} + a_3nx_n = b_{3
. . . . . . . . . . . . . .  . . . . . . . . .   . . . . . . .  . ….. . . . . . . . ..  . . . . . . . . . . . . ..  . . .. .  . .
. . . . . . . . . . . . . .  . . . . . . . . .   . . . . . . .  . ….. . . . . . . . ..  . . . . . . . . . . . . ..  . . .. .  . .}
a_n1x₁ + a_n2x₂ + a_n3x₃ + a_n4x₄ + a_n5x₅ + a_n6x_{6 …….} + a_nnx_n = b_n

در این دستگاه a_ij نشان دهنده ضریب عبارات مجهول x_i است.

معادلات فوق را می توان به صورت ماترسی و به شکل زیر ارائه کرد:

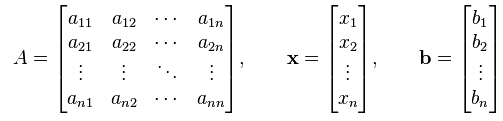
یا اینکه آن را به صورت نوشتاری به شکل [A][X] = [B] در آورد.

حالا با تجزیه ماتریس A به جزء پایین مثلثی و بالا مثلثی این نتیجه را به دست می آوریم:

A = L x U

که در آن:

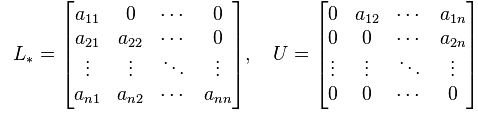
همچنین این دستگاه معادلات خطی را می توان به صورت زیر هم بیان کرد:

L x X = B – UX     —–(a)

در روش گوس سایدل، معادله (a) با حل مقدار سمت چپ x به صورت تکراری و سپس استفاده از مقدار x به دست آمده برای حل سمت راست معادله، حل می شود.

دانلود کنید: ۷ درس کاربردی آموزش برنامه نویسی در متلب

فرایند تکرار در روش گوس سایدل را از لحاظ ریاضی می توان به صورت زیر نوشت:

X^(k+1) = L ^-1( B –UX^(k) )

با استفاده از روش جایگزینی رو به جلو (forward substitution)، عناصر X^(k+1) را می توان به صورت زیر محاسبه کرد:

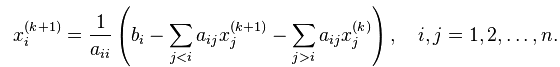
در برنامه متلب نیز همین روال بالا برای این روش استفاده می شود. روند تکرار تا زمانی ادامه می یابد که تغییرات در مقادیر مجهول (x) قابل اغماض و چشم پوشی باشند و یا اینکه به یک میزان خطای تعیین شده دست پیدا کنیم.

روش گوس سایدل در متلب

% Gauss-Seidel Method in MATLAB

function x = gauss_siedel( A ,B )

disp ( ‘Enter the system of linear equations in the form of AX=B’)

%Inputting matrix A

A = input ( ‘Enter matrix A : \n’)

% check if the entered matrix is a square matrix

[na , ma ] = size (A);

if na ~= ma

disp(‘ERROR: Matrix A must be a square matrix’)

return

end

% Inputting matrix B

B = input ( ‘Enter matrix B : ‘)

% check if B is a column matrix

[nb , mb ] = size (B);

if nb ~= na || mb~=1

disp( ‘ERROR: Matrix B must be a column matrix’)

return

end

% Separation of matrix A into lower triangular and upper triangular matrices

% A = D + L + U

D = diag(diag(A));

L = tril(A)- D;

U = triu(A)- D

% check for convergence condition for Gauss-Seidel method

e= max(eig(-inv(D+L)*(U)));

if abs(e) >= 1

disp (‘Since the modulus of the largest Eigen value of iterative matrix is not less than 1’)

disp (‘this process is not convergent.’)

return

end

% initial guess for X..?

% default guess is [ 1 1 …. 1]

r = input ( ‘Any initial guess for X? (y/n): ‘,’s’);

switch r

case ‘y’

% asking for initial guess

X0 = input(‘Enter initial guess for X :\n’)

% check for initial guess

[nx, mx] = size(X0);

if nx ~= na || mx ~= 1

disp( ‘ERROR: Check input’)

return

end

otherwise

X0 = ones(na,1);

end

% allowable error in final answer

t = input ( ‘Enter the error allowed in final answer: ‘);

tol = t*ones(na,1);

k= 1;

X( : , 1 ) = X0;

err= 1000000000*rand(na,1);% initial error assumption for looping

while sum(abs(err) >= tol) ~= zeros(na,1)

X ( : ,k+ 1 ) = -inv(D+L)*(U)*X( : ,k) + inv(D+L)*B;% Gauss-Seidel formula

err = X( :,k+1) – X( :, k);% finding error

k = k + 1;

end

fprintf (‘The final answer obtained after %g iterations is \n’, k)

X( : ,k)

در برنامه متلب بالا، ابتدا یک تابع  x = gauss_siedel( A ,B ) تعریف شده است. در اینجا، A و B ماتریس هایی هستند که با ضرایب استفاده شده در دستگاه معادلات خطی ساخته می شوند. عناصر A و B طبق دستور پایه برنامه نویسی متلب به برنامه وارد می شوند.

حتما بخوانید: آموزش نکات پایه ای و مهم سیمولینک در نرم افزار متلب

A و B باید بررسی شوند: A باید یک ماتریس مربع و B باید یک ماتریس ستونی باشد تا با معیارهای روش گوس سایدل مطابقت داشته باشند. سپس همانطور که قبلا توضیح دادیم، ماتریس A به جزء پایین مثلثی و بالا مثلثی تجزیه می شود تا مقدار تکرار اول به دست بیاید.

برای شروع تکرار دوم از مقدار متغیرهای بدست آمده از تکرار اول استفاده می شود و برنامه تا زمانی که به راه حل مطلوب کاربر برسد به تکرار ادامه می دهد.

در ادامه یک نمونه از صفحه خروجی برنامه متلب را مشاهده می کنید:

مثالی از روش گوس سایدل

ما اینجا برنامه متلب بالا که به روش گوس سایدل بود را به صورت ریاضی حل کرده ایم. معادلات داده شده عبارتند از:

4x₁ – x₂ –x₃ = 3
-2x₁ + 6x₂ + x₃ = 9
-x₁ + x₂ – 7x₃ = -6

برای بدست آوردن مقدار تکرار اول، معادلات داده شده را به صورت زیر بیان می کنیم:

4x₁ – 0 –0 = 3
-2x₁ + 6x₂ + 0 = 9
-x₁ + x₂ – 7x₃ = -6

از معادله اول داریم: x₁ = 3/4 = 0.750

مقدار x₁ را در معادله دوم جایگزین می کنیم:  x₂ = [9 + 2(0.750)] / 6 = 1.750

مقادیر x₁ و x₂ را در معادله سوم جایگزین می کنیم: x₃ = [-6 + 0.750 − 1.750] / 7 = − 1.000

بنابراین نتیجه تکرار اول خواهد بود: (0.750, 1.750, -1.000)

کل فرایند تکراری که در روش گوس سایدل (و برنامه متلب فوق) ادامه دارد در اینجا آورده شده است:

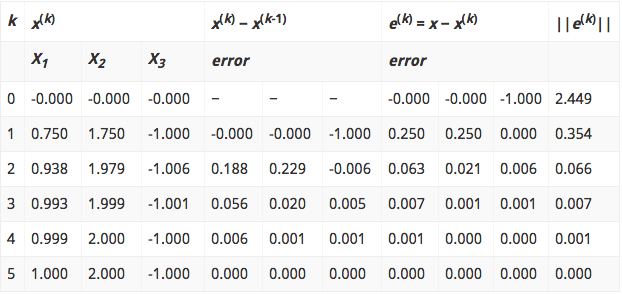
که در آن k تعداد تکرار است.

راه حل نهایی به دست آمده نیز (1.000, 2.000, -1.000) است.

معرفی نرم افزار متلب (۴ کاربرد اصلی و ۳ نقطه قوت)

اگر هنوز هم سوالی درباره روش گوس سایدل یا برنامه متلب دارید، آن را در بخش نظرات همین پست با ما در میان بگذارید.