آموزش مشتق در متلب (به زبان ساده)

مشتق تابع y = f (x) به ما می گوید که چگونه مقدار y نسبت به تغییر x تغییر می کند. به مشتق تابع، شیب تابع نیز گفته می شود.

مشتق تابعf (x) نسبت به متغیر x به صورت زیر نشان داده می شود:

در نرم افزار متلب می توانید مشتق یک تابع را با استفاده از متد diff() به دست آورید.

انواع ساختار متد ()diff عبارتند از:

• diff(f)
• diff(f, a)
• diff(f, b, 2)

تعریف تابع در متلب (ساده ترین روش)

diff(f)

مشتق تابعf (x) را نسبت به متغیر x برمی گرداند.

مثال 1

% Create a symbolic expression in variable x

syms x

f = cos(x);

disp(“f(x) :”);

disp(f);

 % Derivative of f(x)

d = diff(f);

disp(“Derivative of f(x) :”);

disp(d);

خروجی

مثال 2

مشتق تابع را در یک مقدار مشخص برای متغیر x با استفاده از subs(y,x,k) محاسبه می کند.

subs(y,x,k) مقدار تابع y (همان مشتق تابع نسبت به x) را در x = k می دهد.

% Create a symbolic expression in

# variable x

syms x

f = cos(x);

disp(“f(x) :”);

disp(f);

 % Derivative of f(x)

d = diff(f);

val = subs(d,x,pi/2);

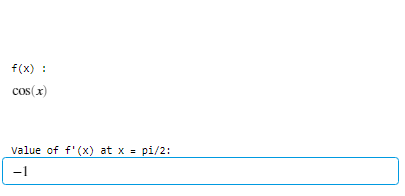
 disp(“Value of f'(x) at x = pi/2:”);

disp(val);

خروجی

diff(f, a)

مشتق تابع f را نسبت به متغیر a برمی گرداند.

مثال

% Create a symbolic expression in variable x

syms x t;

f = sin(x*t);

disp(“f(x) :”);

disp(f);

 % Derivative of f(x,t) wrt t

d = diff(f,t);

متلب رو قورت بده! بدون کلاس، سرعت 2 برابر، ماندگاری 3 برابر، حل ساده سخت ترین پروژه ها، شبیه سازیها و مسائل، فوق العاده پولساز، خرید و دانلود!

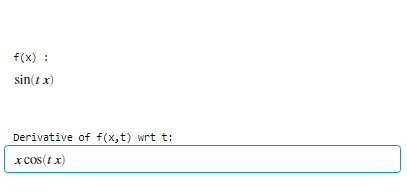
disp(“Derivative of f(x,t) wrt t:”);

disp(d);

خروجی

انتگرال در متلب (آموزش به زبان ساده)

diff(f, b, 2)

مشتق دوم تابع f را نسبت به متغیر b برمی گرداند.

مثال 1

% Create a symbolic expression in

% variable x,n

syms x n;

f = x^n;

disp(“f(x,n) :”);

disp(f);

% Double Derivative of f(x,n) wrt x

d = diff(f,x,2);

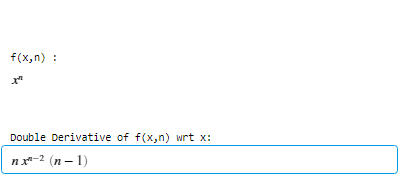
disp(“Double Derivative of f(x,n) wrt x:”);

disp(d);

خروجی

به همین ترتیب می توانید مشتق k ام تابع f را با استفاده از diff(f,x,k) محاسبه کنید.

مثال 2

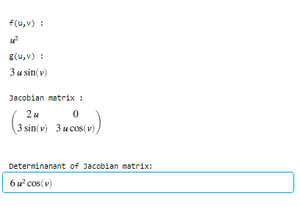
مشتق جزئی زیر را با استفاده از ماتریس ژاکوبین (Jacobian) محاسبه می کند.

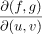
مثال

% Create a symbolic expression in variable

% u and v

syms u v;

f = u^2;

g = sin(v)*(3*u);

disp(“f(u,v) :”);

disp(f);

disp(“g(u,v) :”);

disp(g);

% Jacobian matrix of function f(u,v) and

% g(u,v)

J = jacobian([f; g], [u v]);

disp(“Jacobian matrix :”);

disp(J);

% Determinant of Jacobian matrix

d = det(J);

disp(“Determinant of Jacobian matrix:”);

disp(d);

خروجی

آموزش کامل برنامه نویسی در متلب (22 جلسه رایگان به زبان فارسی)