آموزش مشتقات جزئی ریاضی مهندسی با مثال (به زبان ساده)

رتبه: 0 ار 0 رای sssss

نویسنده: تیم تولید محتوا زمان مطالعه 7 دقیقه

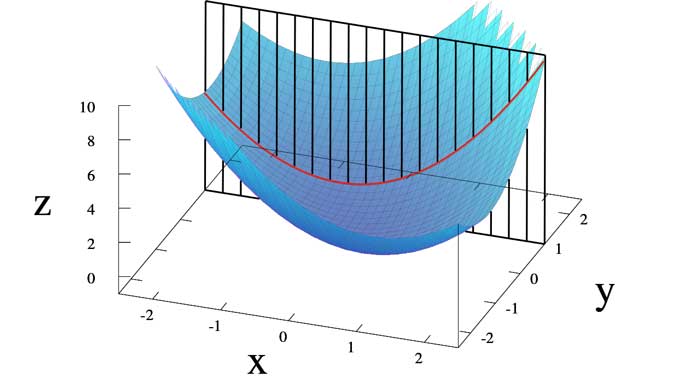
در این مقاله به مشتقات جزئی توابع چند متغیره (به انگلیسی partial derivatives)، می ‌پردازیم. قبل از شروع اجازه بدهید که تعریف مشتق توابع یک متغیره را با هم مرور کنیم. (منبع نوشتار)

مشتق تابع یک متغیره‌ ای به نام f(x) می‌ شود f”(x) که نشان دهنده میزان تغییر تابع نسبت به xها است. اما مشکل یک تابع چند متغیره این است که بیش از یک متغیر دارد. به عبارت دیگر، اگر بخواهیم فقط یکی از متغیر ها تغییر کند یا بخواهیم بیش از یکی از آن ها تغییر کند، چه کار باید بکنیم؟ در واقع، اگر بخواهیم به بیش از یکی از متغیر ها اجازه تغییر بدهیم، راه‌ های زیادی برای تغییرشان وجود خواهد داشت. به طور مثال یک متغیر می ‌تواند سریع تر از متغیر(های) دیگر در تابع تغییر کند. همچنین توجه داشته باشید بسته به این که اجازه بدهیم یک یا چند متغیر چه طور تغییر کنند، تابع و مشتق آن متفاوت خواهد شد.

در این بخش ما به طور انحصاری روی تغییر یکی از متغیر ها در هر لحظه تمرکز می ‌کنیم، طوری که متغیر(های) دیگر ثابت می‌ مانند. در بخش بعدی به چندین متغیر اجازه تغییر خواهیم داد.

حتما دانلود کنید: آموزش صفر تا صد زبان انگلیسی با 32 درس رایگان

از آن جایی که ما فقط به یکی از متغیر ها اجازه تغییر می ‌دهیم، مشتق فرآیند نسبتا ساده‌ ای خواهد بود. اجازه بدهید این بحث را با یک تابع نسبتا ساده شروع کنیم.

بیایید با تابع شروع کرده و میزان تغییر تابع در یک نقطه مثل (a,b) را تعیین کنیم. مثلا y را ثابت نگه داریم و به x اجازه تغییر بدهیم یا برعکس.

ما y را ثابت و x‌ را متغیر در نظر می‌گیریم. از آن جایی که می ‌خواهیم میزان تغییر تابع را در (a,b) را ببینیم و y هم ثابت است، معنایش این است که همیشه y=b خواهد بود. با این کار تابعی داریم که فقط شامل xها می ‌شود و می ‌توانیم یک تابع جدید را به صورت زیر تعریف کنیم :

حالا، این تابع یک متغیره است و در این مرحله تمام چیزی که می ‌خواهیم تعیین میزان تغییر g(x)در x=a است. به عبارت دیگر، ما می ‌خواهیم g′(a) را محاسبه کنیم و از آن جایی که این تابع یک متغیره است، با مشتق‌ گیری اش آشنا هستیم. مشتق تابع در نقطه (a,b) اگر y ثابت و x متغیر باشد ، به این صورت است:

ما به g′(a) مشتق جزئی f(x,y) نسبت به x در نقطه (a,b) می ‌گوییم و آن را به صورت زیر نشان می ‌دهیم:

حالا بیایید این کار را به روش دیگری انجام بدهیم . حالا xها را ثابت و yها را متغیر می ‌گیریم. از آن جا که x ثابت است ، باید x=a باشد. پس می ‌توانیم یک تابع جدید بر حسب y تعریف کنیم و از آن مشتق بگیریم:

در این مورد ما h′(b) را مشتق جزئی f(x,y) بر حسب y در (a,b) می‌نامیم و به صورت زیر نشان می ‌دهیم:

توجه داشته باشید که این دو مشتق جزئی گاهی اوقات مشتقات جزئی مرتبه اول نامیده می ‌شوند. از یک تابع یک متغیره می ‌توانیم چند بار دیگر هم مشتق بگیریم.

به این هم دقت کنید که علامت گذاری مشتقات جزئی با مشتقات توابع یک متغیره متفاوت است . در توابع یک متغیره می ‌توانیم مشتق را با گذاشتن علامت پرایم روی اسم تابع مشخص کنیم. البته در مشتق‌ گیری جزئی همیشه باید متغیری که نسبت به آن مشتق گرفته می ‌شود را به خاطر بسپاریم. به همین خاطر متغیر مورد نظر را زیر تابع می ‌نویسیم. نماد های جایگزینی برای مشتقات جزئی هم هستند که در ادامه معرفی خواهیم کرد.

همچنین توجه داشته باشید که ما معمولا از (a,b) در مشتق‌گیری جزئی که نشان می ‌دهد ما با یک نقطه خاص کار می ‌کنیم، استفاده نمی ‌کنیم. نشانه‌ گذاری استانداردتر این است که فقط از (x,y) استفاده کنیم. با این اوصاف، مشتقات جزئی بالا معمولا به صورت زیر نوشته می‌ شوند:

در حال حاضر، همان طور که این مثال نشان داد، می ‌بینیم که گرفتن مشتق توابع بیشتر از یک متغیره تقریبا به همان روشی انجام می ‌شود که مشتقات یک متغیره انجام می ‌شود. برای محاسبه (x,y) تنها کاری که باید انجام دهید؛ این است که y را مقدار ثابت (یا عدد) در نظر بگیرید و بعد نسبت به xها مثل همیشه مشتق بگیرید. به همین ترتیب، برای محاسبه (x,y) تمام x را مقدار ثابت در نظر بگیرید و سپس نسبت به yها مشتق ‌گیری کنید.

حتما بخوانید: نکات عمومی و پیشرفته ریاضی در نرم افزار متلب

قبل از این که مثالی بزنیم، اجازه بدهید شما را با تعریف رسمی مشتق جزئی و همین طور برخی نماد های جایگزین هم آشنا کنیم.

از آن جایی که می ‌توانیم دو مشتق جزئی بالا را مشتق توابع تک متغیره در نظر بگیریم، نباید این که تعریف رسمی هم شبیه به تعریف مشتق توابع تک متغیره است، خیلی عجیب باشد. دو تابع زیر ، تعاریف رسمی دو مشتق جزئی است که در بالا گفتیم:

f_x (x,y)=〖lim〗_(h→0 ) (f(x+h,y)-f(x,y))/h f_y (x,y)=〖lim〗_(h→0 ) (f(x,y+h)-f(x,y))/h

اگر تعریف حد در حساب و دیفرانسیل 1 را به خاطر بیاورید، این تعریف احتمالا برای تان آشنا به نظر می ‌رسد.

حالا اجازه بدهید نگاهی گذرا به برخی از نماد های جایگزین برای مشتقات جزئی بیندازیم . با توجه به تابع z=f(x,y)، موارد زیر همه معادل هم هستند:

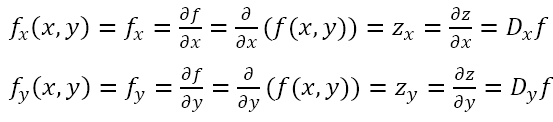
f_x (x,y)=f_x=∂f/∂x=∂/∂x(f(x,y))= z_x=∂z/∂x=D_x f f_y (x,y)=f_y=∂f/∂y=∂/∂y(f(x,y))= z_y=∂z/∂y=D_y f

در نماد کسری مشتق جزئی ، به تفاوت بین مشتق جزئی و مشتق معمولی توجه کنید.

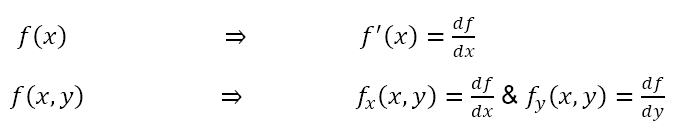
f(x) ⇒ f^' (x)=df/dx f(x,y) ⇒ f_x (x,y)=df/dx & f_y (x,y)=df/dy

خوب، حالا بیایید چند روی چند مثال کار کنیم . هنگام کار روی این مثال‌ ها، همیشه باید به این نکته توجه کنید که نسبت به کدام متغیر مشتق می ‌گیرید. این توجه مهم است زیرا ما تمام متغیر های دیگر را ثابت و مشتق را طوری می ‌گیریم که انگار تابع یک متغیره است. اگر بتوانید این را به خاطر بسپارید، متوجه می ‌شوید که انجام مشتق ‌های جزئی از انجام مشتق ‌های توابع یک متغیره عادی سخت‌ تر نیست.

مثال 2 :

تمام مشتقات جزئی مرتبه اول توابع زیر را محاسبه کنید.

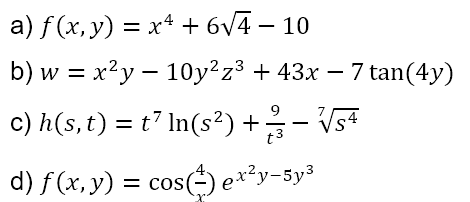
حساب مرد مشتقات جزئی مرتبه اول

دیدید که چند نمونه مشتق جزئی وجود دارد. تا زمانی که یادتان بماند که سایر متغیر ها را ثابت در نظر بگیرید، روش کار دقیقا همان طوری است که در مشتق ‌گیری عادی توابع تک متغیره انجام می ‌شود. بنابراین، اگر می ‌توانید مشتق‌گیری عادی را انجام بدهید، نباید در انجام مشتقات جزئی مشکلی داشته باشید .

یک نکته دیگر هم وجود دارد که در این بخش به صورت گذرا بررسی ‌اش می ‌کنیم و آن هم مشتق ‌گیری ضمنی است. قبل از پرداختن به مشتق ضمنی برای توابع چند متغیره، اول باید مشتق ضمنی مخصوص توابع تک متغیره را به یاد بیاورید . با این مثال شروع کنید .

بلد باشید: آموزش تایپ ریاضی در ورد (و 5 نکته)

مثال 3:

مشتق‌ گیری ضمنی یک تابع چند متغیره هم دقیقا مثل یک متغیره است. اگر تابعی بر حسب سه متغیر x، y و z داشته باشیم، فرض می ‌کنیم که در واقع تابعی بر حسب x و y است یعنی: z=z(x,y)

بنابراین هر گاه از zها را نسبت به x مشتق بگیریم، از قانون زنجیره استفاده کرده ‌ایم و یک اضافه می ‌کنیم. به همین ترتیب، هر زمان که از zها نسبت به y مشتق بگیریم را اضافه می ‌کنیم.