آموزش پردازش سیگنال در متلب 0 تا 100+ PDF رایگان

در دنیای امروز، پردازش سیگنال به عنوان یکی از مهم‌ترین حوزه‌های مهندسی، نقش کلیدی در تحلیل و تفسیر داده‌های متنوع از منابع مختلف مانند صدا، تصویر و داده‌های پزشکی ایفا می‌کند. اهمیت این حوزه با توجه به گسترش فناوری‌های ارتباطی، سیستم‌های هوشمند و اینترنت اشیا بیش از پیش نمایان شده است. MATLAB به عنوان یک ابزار قدرتمند و کاربرپسند در زمینه پردازش سیگنال، امکانات گسترده‌ای برای تحلیل، فیلتر کردن، و استخراج ویژگی‌های سیگنال‌های مختلف فراهم می‌کند.
این نرم‌افزار با ارائه کتابخانه‌های تخصصی و توابع آماده، به کاربران امکان می‌دهد تا به سادگی مفاهیم پایه پردازش سیگنال مانند تبدیل فوریه، فیلترهای دیجیتال و تحلیل حوزه زمان-فرکانس را در پروژه‌های خود به کار گیرند و درک عمیقی از سیگنال‌ها و رفتار آن‌ها کسب کنند.

آشنایی با محیط متلب

نصب و راه‌اندازی متلب

نصب نرم‌افزار متلب (MATLAB) یکی از مراحل اولیه برای شروع کار با این ابزار قدرتمند است. متلب، که مخفف "Matrix Laboratory" است، توسط شرکت MathWorks توسعه داده شده و به عنوان یکی از پرکاربردترین نرم‌افزارها در حوزه مهندسی و علوم کاربردی شناخته می‌شود. برای نصب متلب، ابتدا باید نسخه مناسب برای سیستم‌عامل خود (Windows، macOS، یا Linux) را از سایت رسمی MathWorks دانلود کنید. پس از دانلود فایل نصب، فرآیند نصب با اجرای فایل آغاز می‌شود. این نرم‌افزار با داشتن یک رابط کاربری گرافیکی و نیز امکان اجرای دستورات در محیط خط فرمان، به کاربران امکان می‌دهد تا به‌راحتی با آن کار کنند.

فرآیند نصب شامل چند مرحله است، از جمله پذیرش توافق‌نامه مجوز، انتخاب نوع نصب (Individual یا Network)، انتخاب محل نصب، و وارد کردن اطلاعات حساب MathWorks برای فعال‌سازی نرم‌افزار. در طول نصب، کاربران می‌توانند بسته‌های مختلف توابع و ابزارها را انتخاب کنند تا نصب شوند. این بسته‌ها شامل مجموعه‌ای از توابع کاربردی در زمینه‌های مختلف مانند پردازش سیگنال، پردازش تصویر، کنترل سیستم‌ها و دیگر حوزه‌های مهندسی است. پس از اتمام نصب، متلب آماده استفاده است و می‌توانید آن را از طریق منوی Start یا دسکتاپ اجرا کنید.

پنجره‌های اصلی متلب و نحوه کار با آن‌ها

محیط کاری متلب از چندین پنجره اصلی تشکیل شده است که هر یک وظایف خاص خود را دارند. Command Window  یکی از مهم‌ترین پنجره‌ها است که کاربران می‌توانند در آن دستورات را وارد کرده و نتایج را به صورت فوری مشاهده کنند. این پنجره به عنوان قلب متلب شناخته می‌شود و امکان اجرای دستورات ساده و پیشرفته را فراهم می‌آورد. در کنار این پنجره، Editor  قرار دارد که به کاربران اجازه می‌دهد تا اسکریپت‌ها و توابع خود را در یک محیط ویرایشگر پیشرفته بنویسند. این پنجره ابزارهایی برای نوشتن، ویرایش و اجرای کدها ارائه می‌دهد و به ویژه برای پروژه‌های بزرگ‌تر و پیچیده‌تر مفید است.

یکی دیگر از پنجره‌های مهم Workspace  است که تمام متغیرهای فعلی را که در حافظه هستند نشان می‌دهد. این پنجره اطلاعاتی در مورد نام متغیرها، ابعاد، نوع داده‌ها و مقدار آن‌ها ارائه می‌دهد و به کاربران کمک می‌کند تا متغیرهای خود را مدیریت کنند. Command History  نیز پنجره‌ای است که دستورات اجرا شده در گذشته را ذخیره و نمایش می‌دهد، به کاربران اجازه می‌دهد تا به سرعت دستورات قبلی را بازبینی و دوباره اجرا کنند. Figure Window  نیز یکی دیگر از پنجره‌های کاربردی متلب است که برای نمایش نمودارها و گرافیک‌های تولید شده توسط کاربر استفاده می‌شود. این پنجره به ویژه در پردازش و نمایش سیگنال‌ها اهمیت دارد.

دستورات اولیه و برنامه‌نویسی در متلب

برنامه‌نویسی در متلب با استفاده از دستورات ساده و قدرتمند آن امکان‌پذیر است. برخی از دستورات اولیه شامل تخصیص متغیرها، عملیات ریاضی ساده، و نمایش نتایج است. برای مثال، می‌توانید با استفاده از دستور a = 5 ; متغیری به نام a با مقدار 5 ایجاد کنید. همچنین می‌توانید عملیات ریاضی ساده‌ای مانند جمع و تفریق را انجام دهید، به عنوان مثال، b = a + 3; که مقدار b را برابر با 8 قرار می‌دهد.

متلب همچنین دارای توابع ریاضی گسترده‌ای است که امکان انجام محاسبات پیچیده‌تر را فراهم می‌کند. توابعی مانند sin(x), cos(x), exp(x) و log(x) تنها چند نمونه از توابع موجود در متلب هستند. علاوه بر این، کاربران می‌توانند از دستورات حلقه (for, while) و شرط (if, else) برای نوشتن برنامه‌های پیچیده‌تر استفاده کنند. متلب همچنین اجازه می‌دهد تا توابع دلخواه خود را تعریف کرده و در برنامه‌های مختلف از آن‌ها استفاده کنید. این توابع می‌توانند با استفاده از کلمه کلیدی function تعریف شوند و امکان نوشتن کدهای تمیزتر و قابل استفاده مجدد را فراهم می‌کنند.
دانلود کنید: یادگیری ماشین با پایتون با 12 درس+ کتاب یادگیری ماشین

تولید و نمایش سیگنال‌ها

تولید انواع سیگنال‌های پیوسته و گسسته

یکی از کاربردهای اصلی متلب در حوزه پردازش سیگنال، تولید انواع سیگنال‌های پیوسته و گسسته است. سیگنال‌های پیوسته، سیگنال‌هایی هستند که در تمامی نقاط زمان تعریف شده‌اند، در حالی که سیگنال‌های گسسته فقط در نقاط زمانی معینی تعریف می‌شوند. متلب ابزارهای متعددی برای تولید این سیگنال‌ها در اختیار کاربران قرار می‌دهد.

به عنوان مثال، برای تولید یک سیگنال سینوسی پیوسته می‌توان از دستور زیر استفاده کرد:

t = 0:0.01:2*pi; % تعریف محور زمان

x = sin(t); % تولید سیگنال سینوسی

plot(t, x); % نمایش سیگنال

در این مثال، t بازه زمانی از 0 تا 2π با گام 0.01 تعریف شده است و x سیگنال سینوسی متناظر با این بازه زمانی است. دستور plot سیگنال تولید شده را در حوزه زمان نمایش می‌دهد.

برای تولید سیگنال‌های گسسته مانند سیگنال مربعی، دندانه‌ای یا پالس نیز می‌توان از توابع داخلی متلب استفاده کرد. به عنوان مثال، برای تولید یک سیگنال مربعی گسسته می‌توان از دستور square به صورت زیر استفاده کرد:

t = 0:0.01:2*pi;

x = square(t);

stem(t, x);

در این کد، stem به جای plot استفاده شده است تا ماهیت گسسته سیگنال نمایش داده شود.

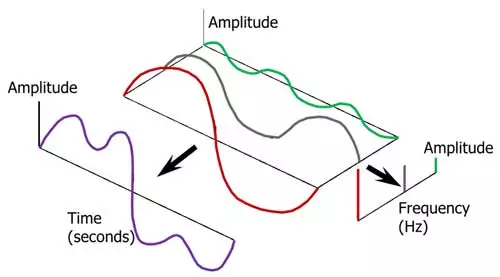
نمایش سیگنال‌ها در حوزه زمان و فرکانس

یکی از ویژگی‌های کلیدی متلب توانایی نمایش سیگنال‌ها در حوزه‌های مختلف است. نمایش سیگنال‌ها در حوزه زمان به سادگی با استفاده از دستور plot امکان‌پذیر است. این دستور نمودار سیگنال را بر حسب زمان رسم می‌کند و به کاربران امکان می‌دهد تا رفتار سیگنال در طول زمان را مشاهده کنند.

نمایش سیگنال‌ها در حوزه فرکانس نیز با استفاده از تبدیل فوریه امکان‌پذیر است. متلب توابعی مانند fft (تبدیل فوریه سریع) را فراهم کرده است که به کاربران امکان می‌دهد سیگنال‌ها را از حوزه زمان به حوزه فرکانس منتقل کرده و تحلیل‌های فرکانسی را انجام دهند. به عنوان مثال، کد زیر نحوه تبدیل یک سیگنال سینوسی به حوزه فرکانس و نمایش آن را نشان می‌دهد:

t = 0:0.01:1;

x = sin(2*pi*50*t) + sin(2*pi*120*t);

y = fft(x);

f = (0:length(y)-1)*100/length(y);

plot(f, abs(y));

در این کد، دو سیگنال سینوسی با فرکانس‌های 50 و 120 هرتز تولید شده و سپس تبدیل فوریه سریع بر روی آن‌ها اعمال می‌شود. نمودار فرکانسی سیگنال با استفاده از plot نمایش داده می‌شود که نشان‌دهنده ترکیب فرکانس‌های موجود در سیگنال است.

پردازش سیگنال در حوزه زمان

نمونه‌برداری و بازسازی سیگنال

نمونه‌برداری یکی از اصول پایه‌ای در پردازش سیگنال است. در نمونه‌برداری، سیگنال پیوسته در زمان‌های گسسته نمونه‌برداری می‌شود تا به یک سیگنال گسسته تبدیل شود. نمونه‌برداری صحیح از سیگنال برای بازسازی دقیق آن اهمیت بسیاری دارد. متلب ابزارهایی برای نمونه‌برداری و بازسازی سیگنال‌ها فراهم کرده است.

برای نمونه‌برداری از یک سیگنال، ابتدا باید نرخ نمونه‌برداری مناسب را انتخاب کنید. به عنوان مثال، برای نمونه‌برداری از یک سیگنال سینوسی با فرکانس 10 هرتز، می‌توانید از کد زیر استفاده کنید:

fs = 100; % نرخ نمونه‌برداری

t = 0:1/fs:1;

x = sin(2*pi*10*t);

stem(t, x);

در اینجا، fs نرخ نمونه‌برداری است و t به عنوان محور زمان گسسته تعریف شده است. سیگنال x نیز نمونه‌برداری شده و با دستور stem نمایش داده شده است.بازسازی سیگنال نیز فرآیندی است که در آن سیگنال گسسته به سیگنال پیوسته تبدیل می‌شود. در متلب، این کار با استفاده از توابع میانگین‌گیری و هموارسازی قابل انجام است. به عنوان مثال، می‌توانید سیگنال نمونه‌برداری شده را به سیگنال پیوسته تبدیل کنید و آن را با سیگنال اصلی مقایسه کنید.

بلد باشید: آموزش گام به گام پردازش سیگنال و تصویر در متلب

اعمال فیلترهای مختلف بر روی سیگنال

فیلترهای دیجیتال ابزارهایی هستند که برای حذف نویز یا استخراج اطلاعات خاص از سیگنال مورد استفاده قرار می‌گیرند. در متلب، می‌توان از فیلترهای مختلفی مانند فیلترهای پایین‌گذر، بالاگذر، و میان‌گذر استفاده کرد. این فیلترها می‌توانند به صورت مستقیم بر روی سیگنال‌ها اعمال شوند.

برای مثال، برای اعمال یک فیلتر پایین‌گذر بر روی یک سیگنال می‌توانید از کد زیر استفاده کنید:

fs = 1000;

t = 0:1/fs:1-1/fs;

x = sin(2*pi*50*t) + sin(2*pi*120*t);

d = designfilt('lowpassfir', 'PassbandFrequency', 0.15, 'StopbandFrequency', 0.2);

y = filter(d, x);

plot(t, x, t, y);

در این کد، دو سیگنال سینوسی با فرکانس‌های 50 و 120 هرتز تولید شده و سپس فیلتر پایین‌گذر بر روی آن‌ها اعمال می‌شود. سیگنال فیلتر شده y و سیگنال اصلی x با هم نمایش داده می‌شوند تا تاثیر فیلتر بر سیگنال مشاهده شود.

عملیات ریاضی بر روی سیگنال‌ها

عملیات ریاضی مختلفی می‌توان بر روی سیگنال‌ها در متلب انجام داد. این عملیات شامل جمع، تفریق، ضرب و تقسیم سیگنال‌ها است. به عنوان مثال، می‌توان دو سیگنال سینوسی را با هم جمع کرد تا یک سیگنال ترکیبی ایجاد شود. این عملیات به سادگی با استفاده از دستورات متلب امکان‌پذیر است.

برای مثال، کد زیر نحوه جمع دو سیگنال سینوسی را نشان می‌دهد:

t = 0:0.01:1;

x1 = sin(2*pi*10*t);

x2 = sin(2*pi*20*t);

x = x1 + x2;

plot(t, x1, t, x2, t, x);

در این کد، دو سیگنال سینوسی x1 و x2 تولید شده و سپس با هم جمع می‌شوند تا سیگنال x به دست آید. نمودار سیگنال‌های جداگانه و ترکیبی نمایش داده می‌شود تا تاثیر عملیات جمع بر سیگنال‌ها مشاهده شود.

پردازش سیگنال در حوزه فرکانس

تبدیل فوریه گسسته (DFT) و تبدیل فوریه سریع (FFT)

تبدیل فوریه یکی از ابزارهای اصلی برای تحلیل سیگنال‌ها در حوزه فرکانس است. تبدیل فوریه گسسته (DFT) و تبدیل فوریه سریع (FFT) به ترتیب دو روش برای انجام این تحلیل‌ها هستند. متلب توابع داخلی برای هر دو نوع تبدیل فراهم کرده است که امکان تحلیل سیگنال‌ها را در حوزه فرکانس فراهم می‌کنند.

برای مثال، کد زیر نحوه انجام تبدیل فوریه سریع بر روی یک سیگنال را نشان می‌دهد:

t = 0:0.001:1-0.001;

x = cos(2*pi*100*t) + sin(2*pi*200*t);

y = fft(x);

f = (0:length(y)-1)*(1/max(t));

plot(f, abs(y));

در این کد، سیگنال x شامل دو مؤلفه فرکانسی 100 و 200 هرتز است. تبدیل فوریه سریع بر روی این سیگنال اعمال می‌شود و نمودار فرکانسی آن نمایش داده می‌شود که شامل پیک‌هایی در فرکانس‌های 100 و 200 هرتز است.

فوق العاده کاربردی: پردازش صدا در متلب (آموزش کامل و نکات کاربردی)

تحلیل طیف فرکانسی سیگنال‌ها

پس از انجام تبدیل فوریه، تحلیل طیف فرکانسی سیگنال‌ها انجام می‌شود تا ویژگی‌های فرکانسی سیگنال‌ها شناسایی شوند. تحلیل طیف فرکانسی به کاربران کمک می‌کند تا اطلاعاتی درباره فرکانس‌های موجود در سیگنال و قدرت هر یک از آن‌ها به دست آورند. این تحلیل به ویژه در کاربردهایی مانند مخابرات، پردازش صوت و پردازش تصویر مفید است.

کاربردهای پردازش سیگنال

پردازش صوت

یکی از مهم‌ترین کاربردهای پردازش سیگنال در حوزه پردازش صوت است. متلب ابزارهای مختلفی برای تحلیل و پردازش سیگنال‌های صوتی ارائه می‌دهد که می‌توانند در سیستم‌های شناسایی گفتار، کاهش نویز، و بهبود کیفیت صدا استفاده شوند. برای مثال، می‌توان با استفاده از متلب، سیگنال صوتی را فیلتر کرد تا نویزهای ناخواسته حذف شوند.

پردازش تصویر

پردازش تصویر نیز یکی دیگر از حوزه‌های مهم پردازش سیگنال است. در این حوزه، سیگنال‌ها به صورت تصاویر دوبعدی تعریف می‌شوند و می‌توان با استفاده از توابع متلب، تصاویر را تحلیل، بهبود و فیلتر کرد. متلب ابزارهایی برای پردازش تصاویر ارائه می‌دهد که به کاربران اجازه می‌دهد تا عملیاتی مانند تغییر اندازه، فیلترگذاری، و استخراج ویژگی‌ها را انجام دهند.

پردازش داده‌های بیولوژیکی

در حوزه پزشکی، پردازش سیگنال‌های بیولوژیکی مانند سیگنال‌های قلبی (ECG) و مغزی (EEG) از اهمیت بالایی برخوردار است. متلب امکانات گسترده‌ای برای پردازش و تحلیل این سیگنال‌ها فراهم کرده است. برای مثال، می‌توان با استفاده از متلب، سیگنال ECG را تحلیل کرد تا اطلاعاتی درباره وضعیت قلب بیمار به دست آورد.

مخابرات

پردازش سیگنال در مخابرات برای انتقال و دریافت اطلاعات ضروری است. سیگنال‌های مخابراتی باید به طور صحیح نمونه‌برداری، فیلتر و مدوله شوند تا اطلاعات به درستی منتقل شوند. متلب ابزارهای متعددی برای پردازش سیگنال‌های مخابراتی ارائه می‌دهد که می‌توانند در طراحی و تحلیل سیستم‌های مخابراتی استفاده شوند.

کنترل سیستم‌ها

در سیستم‌های کنترلی، پردازش سیگنال برای کنترل دقیق و پایدار سیستم‌ها استفاده می‌شود. متلب امکانات گسترده‌ای برای طراحی و شبیه‌سازی سیستم‌های کنترلی فراهم کرده است. پردازش سیگنال‌های حسگرها و اعمال کنترل‌های مناسب بر روی سیستم، از کاربردهای مهم متلب در این حوزه است.

فیلترهای دیجیتال

طراحی فیلترهای FIR و IIR

فیلترهای دیجیتال به دو دسته اصلی FIR (Finite Impulse Response) و IIR (Infinite Impulse Response) تقسیم می‌شوند. فیلترهای FIR از نظر پایداری مزیت‌هایی دارند، زیرا پاسخ ضربه‌ای آن‌ها محدود است و همیشه پایدار هستند. فیلترهای IIR از نظر بهره‌وری در استفاده از حافظه و زمان محاسباتی بهینه‌تر هستند، اما ممکن است ناپایدار شوند. متلب ابزارهای متعددی برای طراحی هر دو نوع فیلتر ارائه می‌دهد.

برای طراحی یک فیلتر FIR، می‌توان از دستور fir1 استفاده کرد. به عنوان مثال، برای طراحی یک فیلتر پایین‌گذر FIR با 20 ضرایب و فرکانس قطع 0.5 (نرمال‌شده به نرخ نمونه‌برداری) می‌توان کد زیر را استفاده کرد:

n = 20;

cutoff = 0.5;

b = fir1(n, cutoff);

freqz(b, 1);

این کد فیلتر FIR را طراحی کرده و پاسخ فرکانسی آن را با استفاده از freqz نمایش می‌دهد.
دانلود کنید که دیگه گیرتون نمیاد! آموزش کامل برنامه نویسی در متلب (22 جلسه رایگان به زبان فارسی)

روش‌های مختلف طراحی فیلتر Butterworth)، Chebyshev، Elliptic و …)

روش‌های مختلفی برای طراحی فیلترهای دیجیتال وجود دارد، که هر یک ویژگی‌ها و کاربردهای خاص خود را دارند. فیلترهای Butterworth، Chebyshev و Elliptic از رایج‌ترین روش‌ها هستند. فیلتر Butterworth دارای یک پاسخ فرکانسی صاف و یکنواخت است، در حالی که فیلترهای Chebyshev و Elliptic با استفاده از اجازه دادن به ریزموج‌ها در نوار عبور یا توقف، شیب‌های تیزتری دارند.

برای طراحی یک فیلتر Butterworth، می‌توان از دستور butter استفاده کرد. به عنوان مثال، کد زیر نحوه طراحی یک فیلتر پایین‌گذر Butterworth از مرتبه 4 با فرکانس قطع 0.5 را نشان می‌دهد:

n = 4;

cutoff = 0.5;

[b, a] = butter(n, cutoff);

freqz(b, a);

این کد ضرایب فیلتر را محاسبه کرده و پاسخ فرکانسی آن را نمایش می‌دهد.

تحلیل طیفی

روش‌های مختلف تخمین طیف (پریودوگرام، Welch، Bartlett)

تحلیل طیفی سیگنال‌ها یکی از کاربردهای مهم پردازش سیگنال است. پریودوگرام یکی از ساده‌ترین روش‌های تخمین طیف است که به سادگی با استفاده از تبدیل فوریه سریع (FFT) و نمایش قدرتمند طیف فرکانسی به دست می‌آید. این روش سریع و کارآمد است، اما ممکن است دارای نوسانات بالایی باشد.

روش Welch به عنوان بهبود یافته پریودوگرام معرفی شده است. در این روش، سیگنال به چندین بخش تقسیم شده و روی هر بخش به صورت جداگانه FFT اعمال می‌شود. سپس طیف‌های به دست آمده میانگین‌گیری می‌شوند تا تخمین طیف نهایی حاصل شود. این روش نوسانات را کاهش داده و دقت تخمین طیف را افزایش می‌دهد.

روش Bartlett نیز مشابه روش Welch است، اما در آن از میانگین‌گیری ساده بر روی بخش‌های مختلف سیگنال استفاده می‌شود.

آموزش نکات پایه ای و مهم سیمولینک در نرم افزار متلب

پردازش سیگنال‌های تصادفی

فرایندهای تصادفی و ویژگی‌های آن‌ها

فرایندهای تصادفی به عنوان مجموعه‌ای از متغیرهای تصادفی تعریف می‌شوند که می‌توانند به عنوان مدل‌هایی برای سیگنال‌های واقعی مورد استفاده قرار گیرند. سیگنال‌های تصادفی ممکن است شامل نویزها یا داده‌های غیرقطعی باشند که در سیستم‌های واقعی مشاهده می‌شوند. تحلیل و پردازش سیگنال‌های تصادفی برای درک رفتار آن‌ها و استخراج اطلاعات مفید ضروری است.

فیلتر کردن سیگنال‌های تصادفی

یکی از کاربردهای مهم پردازش سیگنال‌های تصادفی، فیلتر کردن آن‌ها برای کاهش نویز یا استخراج اطلاعات مفید است. فیلترهای دیجیتال مانند فیلترهای کالمن و Wiener ابزارهای کارآمدی برای پردازش سیگنال‌های تصادفی هستند. متلب ابزارهای متعددی برای پیاده‌سازی این فیلترها ارائه می‌دهد.

پردازش سیگنال‌های چند بعدی

پردازش تصویر با استفاده از متلب

پردازش تصویر به عنوان یکی از مهم‌ترین کاربردهای پردازش سیگنال‌های چندبعدی شناخته می‌شود. تصاویر به عنوان سیگنال‌های دو بعدی تعریف می‌شوند که می‌توان آن‌ها را با استفاده از توابع متلب تحلیل، بهبود و فیلتر کرد. متلب ابزارهای متعددی برای پردازش تصاویر فراهم کرده است که به کاربران اجازه می‌دهد تا عملیاتی مانند تغییر اندازه، فیلترگذاری، و استخراج ویژگی‌ها را انجام دهند.

تبدیل فوریه دو بعدی و کاربردهای آن

تبدیل فوریه دو بعدی یکی از ابزارهای مهم در پردازش تصویر است. این تبدیل به کاربران امکان می‌دهد تا تصاویر را از حوزه مکان به حوزه فرکانس منتقل کرده و تحلیل‌های فرکانسی را انجام دهند. برای مثال، می‌توان با استفاده از تبدیل فوریه دو بعدی، نویزهای فرکانسی را از تصاویر حذف کرد یا ویژگی‌های خاصی را در آن‌ها شناسایی کرد. متلب توابع داخلی برای انجام این تبدیل فراهم کرده است.

دانلود PDF های گلچین شده پردازش سیگنال متلب

  دانلود کتاب گلچین شده از وب (حدود 12 مگابایت)

جمع بندی و یک نکته تکمیلی

در این مقاله، به بررسی جامع و کاملی از پردازش سیگنال‌ها با استفاده از نرم‌افزار متلب پرداخته شد. ابتدا با محیط متلب و نحوه نصب و راه‌اندازی آن آشنا شدیم و پنجره‌ها و دستورات اولیه آن را معرفی کردیم. سپس به تولید و نمایش انواع سیگنال‌های پیوسته و گسسته و تحلیل آنها در حوزه زمان و فرکانس پرداختیم. مراحل مهمی مانند نمونه‌برداری، بازسازی سیگنال، اعمال فیلترهای مختلف و انجام عملیات ریاضی بر روی سیگنال‌ها در حوزه زمان بررسی شد.
در ادامه، مفاهیم تبدیل فوریه گسسته و سریع و تحلیل طیف فرکانسی سیگنال‌ها را بررسی کرده و کاربردهای مختلف پردازش سیگنال در زمینه‌هایی چون پردازش صوت، تصویر، داده‌های بیولوژیکی، مخابرات و کنترل سیستم‌ها را مرور کردیم. همچنین، به بررسی فیلترهای دیجیتال و روش‌های مختلف طراحی آنها، تحلیل طیفی، پردازش سیگنال‌های تصادفی و پردازش سیگنال‌های چند بعدی پرداختیم.

اینو یاد بگیرید: آموزش شبکه عصبی در متلب

این مباحث به طور کامل نشان داد که پردازش سیگنال‌ها با استفاده از متلب، ابزاری قدرتمند و انعطاف‌پذیر برای تحلیل، فیلترگذاری، و استخراج اطلاعات از داده‌های مختلف است. با استفاده از این دانش و ابزارهای معرفی‌شده، می‌توان پروژه‌های پیچیده و کاربردی در حوزه‌های مختلف علمی و صنعتی را با دقت بالا و بهینه‌سازی قابل توجه انجام داد.