آموزش ایجاد ماتریس در متلب (و نکات و عملیات ها)

MATLAB مخفف “آزمایشگاه ماتریس” است. در حالی که سایر زبانهای برنامه نویسی عمدتا با اعداد یک به یک کار می کنند ، MATLAB® به گونه ای طراحی شده است که اساساً روی کل ماتریس ها و آرایه ها کار می کند.

همه متغیرهای MATLAB ، بدون توجه به نوع داده ، آرایه های چند بعدی هستند. ماتریس یک آرایه دو بعدی است که اغلب برای جبر خطی استفاده می شود.

۷ درس کاربردی آموزش برنامه نویسی در متلب (فیلم+زبان فارسی)

ایجاد آرایه

برای ایجاد یک آرایه با چهار عنصر در یک ردیف ، عناصر را با یک کاما (،) یا یک فاصله جدا کنید.

a = [1 2 3 4]

a = 1×4

1 2 3 4

این نوع آرایه بردار سطر است.

برای ایجاد ماتریسی که چندین ردیف داشته باشد ، ردیف ها را با علامت های نقطه ویرگول جدا کنید.

a = [1 3 5; 2 4 6; 7 8 10]

a = 3×3

1 3 5

2 4 6

7 8 10

روش دیگر برای ایجاد ماتریس استفاده از تابعی مانند یک ، صفر یا rand است. به عنوان مثال ، یک بردار ستون 5 در 1 صفر ایجاد کنید.

z = zeros(5,1)

z = 5×1

0

0

0

0

0

عملیات ماتریس و آرایه

MATLAB به شما این امکان را می دهد که با استفاده از یک عملگر یا تابع حساب ، همه مقادیر را در یک ماتریس پردازش کنید.

a + 10

ans = 3×3

11 13 15

12 14 16

17 18 20

sin(a)

ans = 3×3

0.8415 0.1411 -0.9589

0.9093 -0.7568 -0.2794

0.6570 0.9894 -0.5440

برای جابجایی ماتریس ، از یک نقل قول (‘) استفاده کنید:

a’

ans = 3×3

1 2 7

3 4 8

5 6 10

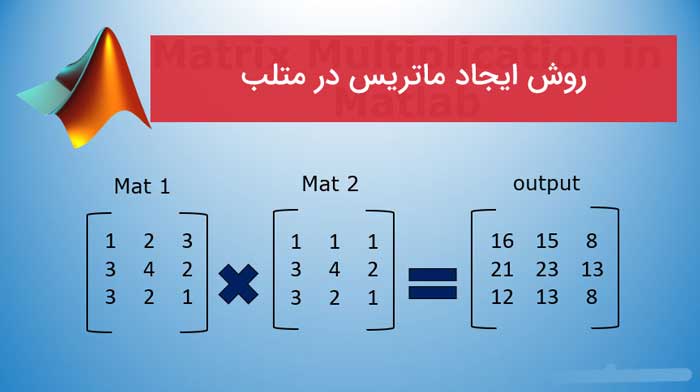
با استفاده از عملگر * می توانید ضرب ماتریس استاندارد ، که محاسبه محصولات داخلی بین سطرها و ستون ها است ، انجام دهید. به عنوان مثال ، تأیید کنید که یک ماتریس معکوس آن ماتریس واحد را برمی گرداند:

p = a*inv(a)

p = 3×3

1.0000 0 0

0 1.0000 0

0 -0.0000 1.0000

توجه داشته باشید که p ماتریسی از مقادیر صحیح نیست. MATLAB اعداد را به عنوان مقادیر نقطه شناور ذخیره می کند و عملیات حسابی نسبت به تفاوت های کوچک بین مقدار واقعی و نمایش نقطه شناور آن حساس هستند. با استفاده از دستور format می توانید رقم اعشار بیشتری نمایش دهید:

format long

p = a*inv(a)

p = 3×3

0.999999999999996 0 0

0 1.000000000000000 0

0 -0.000000000000014 1.000000000000000

با استفاده از این نمایشگر را به قالب کوتاه تر تنظیم کنید

format short

متلب رو قورت بده! بدون کلاس، سرعت 2 برابر، ماندگاری 3 برابر، حل ساده سخت ترین پروژه ها، شبیه سازیها و مسائل، فوق العاده پولساز، خرید و دانلود!

Format فقط نمایش اعداد را تحت تأثیر قرار می دهد ، نه نحوه محاسبه یا ذخیره MATLAB.

برای انجام ضرب با عنصر به جای ضرب ماتریس ، از عملگر .* استفاده کنید

p = a.*a

p = 3×3

1 9 25

4 16 36

49 64 100

عملگرهای ماتریس برای ضرب ، تقسیم و توان هر یک دارای یک عملگر آرایه متناظر هستند که با توجه به عناصر عمل می کند. به عنوان مثال ، هر عنصر a را به توان سه برسانید:

a.^3

ans = 3×3

1 27 125

8 64 216

343 512 1000

الحاق (concatenation)

الحاق فرآیند پیوستن به آرایه ها برای بزرگتر کردن است. در واقع ، شما اولین آرایه خود را با هم پیوند دادن عناصر جداگانه آن ایجاد کردید. جفت براکت مربع [] عملگر اتصال است.

A = [a,a]

A = 3×6

1 3 5 1 3 5

2 4 6 2 4 6

7 8 10 7 8 10

آرایه های متصل به هم با استفاده از ویرگول را horizental concatenation یا الحاق افقی می گویند. هر آرایه باید به همان تعداد ردیف باشد. به همین ترتیب ، وقتی آرایه ها تعداد ستون های یکسانی دارند ، می توانید با استفاده از نقطه ویرگول به صورت عمودی بهم بپیوندید.

A = [a; a]

A = 6×3

1 3 5

2 4 6

7 8 10

1 3 5

2 4 6

7 8 1

اعداد مختلط

اعداد مختلط دارای هر دو بخش واقعی و خیالی هستند ، جایی که واحد خیالی ریشه مربع1- است.

sqrt(-1)

ans = 0.0000 + 1.0000i

برای نمایش بخش خیالی اعداد مختلط ، از i یا j استفاده کنید.

c = [3+4i, 4+3j; -i, 10j]

c = 2×2 complex

3.0000 + 4.0000i 4.0000 + 3.0000i

0.0000 – 1.0000i 0.0000 +10.0000i

آموزش اسکریپت در متلب (به زبان ساده)

جمع بندی و نکات تکمیلی مهم

۲. ایجاد ماتریس در متلب

الف. ایجاد ماتریس دستی

• ماتریس ساده: برای ایجاد یک ماتریس، عناصر را درون براکت‌ها قرار دهید و سطرها را با سمیکالن (;) جدا کنید.

  A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

  این کد یک ماتریس ۳x۳ ایجاد می‌کند.

• ماتریس با اعداد تصادفی: برای ایجاد یک ماتریس با اعداد تصادفی، از تابع rand استفاده کنید.

  B = rand(3, 3);  % ماتریس ۳x۳ با اعداد تصادفی بین ۰ و ۱

ب. ایجاد ماتریس با توابع خاص

• ماتریس صفر: برای ایجاد یک ماتریس پر از صفر، از تابع zeros استفاده کنید.

  C = zeros(2, 3);  % ماتریس ۲x۳ پر از صفر

• ماتریس یک: برای ایجاد یک ماتریس پر از یک، از تابع ones استفاده کنید.

  D = ones(3, 2);  % ماتریس ۳x۲ پر از یک

• ماتریس واحد (Identity Matrix):
  برای ایجاد یک ماتریس واحد، از تابع eye استفاده کنید.

  E = eye(4);  % ماتریس واحد ۴x۴

۳. عملیات پایه‌ای روی ماتریس‌ها

الف. دسترسی به عناصر ماتریس

• دسترسی به یک عنصر: برای دسترسی به یک عنصر خاص، از اندیس‌های سطر و ستون استفاده کنید.

  A = [1, 2, 3; 4, 5, 6; 7, 8, 9];
  element = A(2, 3);  % عنصر در سطر ۲ و ستون ۳ (مقدار ۶)

• دسترسی به یک سطر یا ستون: برای دسترسی به یک سطر یا ستون کامل، از عملگر : استفاده کنید.

  row = A(2, :);  % سطر دوم (ماتریس [4, 5, 6])
  column = A(:, 3);  % ستون سوم (ماتریس [3; 6; 9])

ب. تغییر اندازه ماتریس

• تغییر اندازه: برای تغییر اندازه ماتریس، از تابع reshape استفاده کنید.

  A = [1, 2, 3; 4, 5, 6];
  B = reshape(A, 3, 2);  % تغییر اندازه به ماتریس ۳x۲

ج. الحاق ماتریس‌ها

• الحاق افقی: برای الحاق دو ماتریس به صورت افقی، از عملگر , یا تابع horzcat استفاده کنید.

  A = [1, 2; 3, 4];
  B = [5, 6; 7, 8];
  C = [A, B];  % الحاق افقی

• الحاق عمودی: برای الحاق دو ماتریس به صورت عمودی، از عملگر ; یا تابع vertcat استفاده کنید.

  D = [A; B];  % الحاق عمودی

۴. عملیات ریاضی روی ماتریس‌ها

الف. جمع و تفریق ماتریس‌ها

• جمع:
  برای جمع دو ماتریس، از عملگر + استفاده کنید.

  A = [1, 2; 3, 4];
  B = [5, 6; 7, 8];
  C = A + B;

• تفریق: برای تفریق دو ماتریس، از عملگر - استفاده کنید.

  D = A - B;

ب. ضرب ماتریس‌ها

• ضرب عنصر به عنصر: برای ضرب عنصر به عنصر دو ماتریس، از عملگر .* استفاده کنید.

  E = A .* B;

• ضرب ماتریسی: برای ضرب ماتریسی، از عملگر * استفاده کنید.

  F = A * B;

ج. ترانهاده ماتریس

• ترانهاده: برای محاسبه ترانهاده یک ماتریس، از عملگر ' استفاده کنید.

  G = A';

۵. توابع مفید برای کار با ماتریس‌ها

الف. محاسبه دترمینان

• دترمینان: برای محاسبه دترمینان یک ماتریس مربعی، از تابع det استفاده کنید.

  det_A = det(A);

ب. محاسبه معکوس ماتریس

• معکوس: برای محاسبه معکوس یک ماتریس مربعی، از تابع inv استفاده کنید.

  inv_A = inv(A);

ج. محاسبه مقادیر ویژه و بردارهای ویژه

• مقادیر ویژه: برای محاسبه مقادیر ویژه و بردارهای ویژه، از تابع eig استفاده کنید.

  [V, D] = eig(A);  % V: بردارهای ویژه، D: مقادیر ویژه