عدد مختلط در متلب، اندازه و رسم نمودار مختلط (آموزش به زبان ساده)

این مطلب نشان می‌دهد که چگونه می‌توان اعداد مختلط را در MATLAB ترسیم کرد. یک عدد مختلط z عددی است که می‌توان آن را به صورت

yi+x=z

نوشت، که در آن x  و y  اعداد حقیقی هستند و i  واحد موهومی است که به صورت   i²=-1  تعریف می‌شود. عدد  x بخش حقیقی عدد مختلط است که به صورت x=Re(z)  نشان داده می‌شود، و عدد y بخش موهومی عدد مختلط است که به صورت y=Im(z) نشان داده می‌شود. شما می‌توانید یک عدد مختلط را به صورت یک جفت مختصات (x,y)  در صفحه مختلط، که به آن نمودار آرگاند نیز می‌گویند، ترسیم کنید. در این نمودار، از مختصات دکارتی برای نمایش بخش حقیقی در محور x  و بخش موهومی در محور y  استفاده می‌شود.

همچنین می‌توانید یک عدد مختلط را با استفاده از نمایش قطبی نشان دهید. عدد مختلط به صورت زیر نوشته می‌شود (دقت کنید ^ به معنی توان است):
z=re^iθ=r(cosθ+i sinθ)

که در آن r مقدار مطلق یا اندازه عدد مختلط است و θ  زاویه فاز عدد مختلط است. در این نمایش، می‌توانید یک عدد مختلط را به صورت یک نقطه در مختصات قطبی با شعاع r  (فاصله از مبدا) و زاویه قطبی θ (زاویه پادساعتگرد بین محور حقیقی مثبت و خط متصل کننده نقطه به مبدا) ترسیم کنید.

ترسیم آرایه‌ای از اعداد مختلط

یک بردار ایجاد کنید که شامل اعداد مختلط  3 + 4i, -4 - 3i, 1 - 2i, و -1 - 1i .

z = [3 + 4i; -4 - 3i; 1 - 2i; -1 - 1i]

خروجی:

z = 4×1 complex

   3.0000 + 4.0000i

  -4.0000 - 3.0000i

   1.0000 - 2.0000i

  -1.0000 - 1.0000i

بخش موهومی را در برابر بخش حقیقی بردار مختلط z  با استفاده از دستور plot  ترسیم کنید. از توابع real  و imag  برای بازگرداندن بخش‌های حقیقی و موهومی بردار مختلط به ترتیب استفاده کنید.

plot(real(z), imag(z), "o")

axis equal

grid on

xlabel("Re(z)")

ylabel("Im(z)")

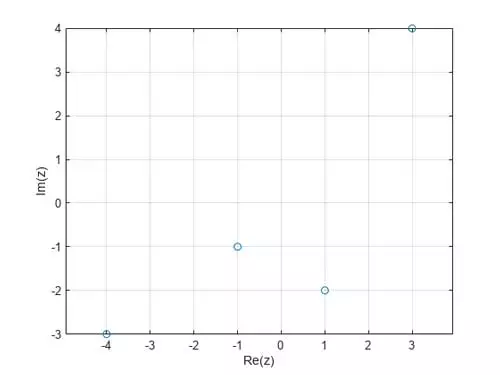
همچنین می‌توانید به جای استفاده از plot(real(z) , imag(z), LineSpec) از plot(z, LineSpec)  برای ترسیم یک آرایه از اعداد مختلط استفاده کنید. این تابع به طور خودکار بخش حقیقی را در محور xxx و بخش موهومی را در محور y  ترسیم می‌کند.

ترسیم ریشه‌های مختلط وحدت در مختصات دکارتی

ریشه‌های nام وحدت، اعداد مختلطی هستند که معادله چندجمله‌ای زیر را برآورده می‌کنند:

که در آن n  یک عدد صحیح مثبت است.

ریشه‌های nام وحدت به صورت زیر هستند:
exp⁡(2kπi/n)=cos(2kπ/n)+isin 2kπ/n,for k=0,1,…,n-1

برای یافتن ریشه‌های مختلط وحدت، می‌توانید معادله چندجمله‌ای را با استفاده از تابع roots حل کنید. تابع roots معادلات چندجمله‌ای به صورت   p₁xⁿ+…+p_nx+p_n+1 را حل می‌کند. به عنوان مثال، ریشه‌های پنجم وحدت برای معادلهz⁵=1  یا  z⁵-1=0   را پیدا کنید.

p = [1 0 0 0 0 -1];

z = roots(p)

خروجی:

z = 5×1 complex

  -0.8090 + 0.5878i

  -0.8090 - 0.5878i

   0.3090 + 0.9511i

   0.3090 - 0.9511i

   1.0000 + 0.0000i

ریشه‌های مختلط وحدت را در مختصات دکارتی ترسیم کنید.

plot(z, "o")

axis equal

grid on

xlabel("Re(z)")

ylabel("Im(z)")

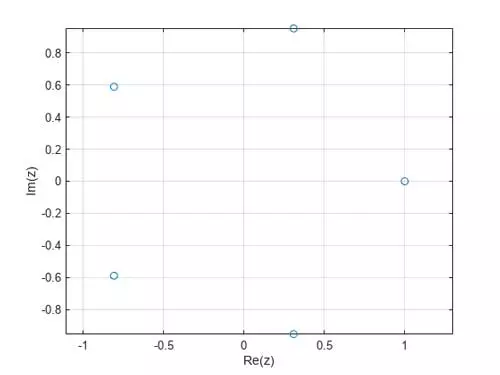
رسم اعداد مختلط در مختصات قطبی

ریشه‌های پنجم وحدت را در مختصات قطبی با استفاده از polarplot ترسیم کنید. از تابع angle برای بازگرداندن زوایای فاز ریشه‌های مختلط و از تابع abs برای بازگرداندن مقادیر مطلق یا شعاع‌های ریشه‌های مختلط استفاده کنید.

polarplot(angle(z), abs(z), "o")

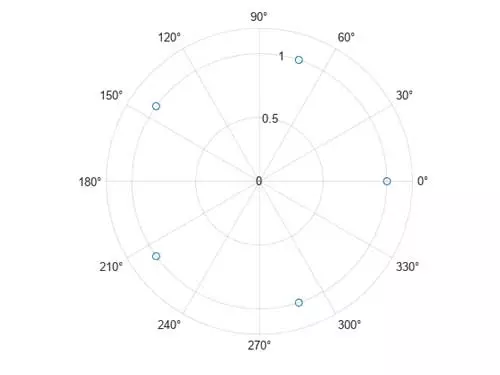
همچنین می‌توانید به جای استفاده از  polarplot(angle(z) , abs(z), linespec) از  polarplot(z, linespec) برای ترسیم یک آرایه از اعداد مختلط در مختصات قطبی استفاده کنید. این تابع به طور خودکار شعاع‌ها و زوایای فاز اعداد مختلط را ترسیم می‌کند.

دانلود کنید: آموزش پردازش سیگنال در متلب 0 تا 100+ PDF رایگان

ترسیم منحنی پارامتریک در صفحه مختلط

یک منحنی پارامتریک تعریف کنید که به صورت زیر است:

exp⁡(it).t=f(t)=z

که پارامتر t  در بازه [0,4π]  قرار دارد.

یک بردار t  با 200 نقطه به طور یکنواخت در این بازه ایجاد کنید تا t  پارامتریزه شود. نقاطی که روی منحنی مختلط قرار دارند را به صورت یک بردار مختلط z  تعریف کنید.

t = linspace(0, 4*pi, 200);

z = t.*exp(1i*t);

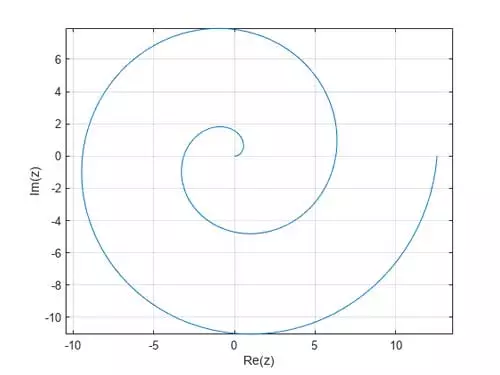
منحنی مختلط را در مختصات دکارتی ترسیم کنید.

plot(z, "-")

axis equal

grid on

xlabel("Re(z)")

ylabel("Im(z)")

منحنی مختلط را در مختصات قطبی ترسیم کنید.

polarplot(z, "-")

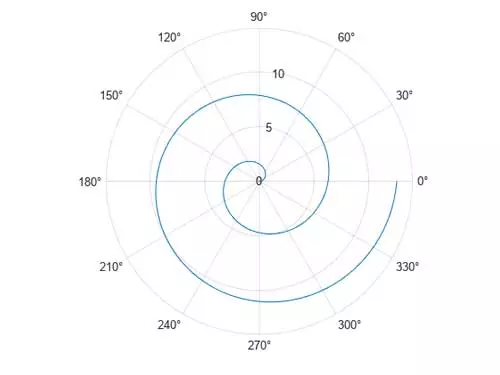
یک ماتریس مربعی n×n  واقعی دارای n مقدار ویژه (با در نظر گرفتن چندگانگی جبری) است که یا واقعی هستند یا به صورت جفت‌های مزدوج مختلط ظاهر می‌شوند.

به عنوان مثال، یک ماتریس واقعی 20×20 با عناصر تصادفی که از یک توزیع نرمال استاندارد نمونه‌گیری شده‌اند، در نظر بگیرید. مقادیر ویژه را با استفاده از eig  محاسبه کنید.

rng("default")

z = eig(randn(20));

دانلود کنید: دانلود 2 کتاب محاسبات عددی با متلب (PDF رایگان)

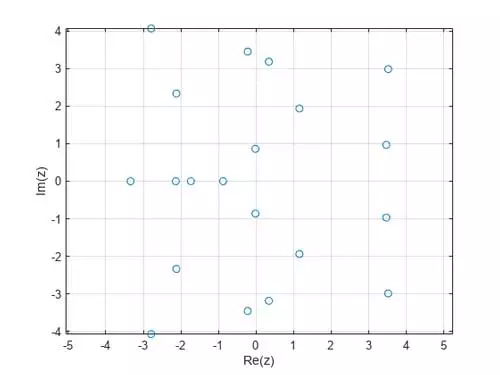
بخش موهومی را در برابر بخش حقیقی تمام 20 مقدار ویژه ترسیم کنید. توجه کنید که برای هر مقدار ویژه z_k=x_k+y_ki  که روی محور حقیقی نیست، یک جفت مزدوج مختلط از این مقدار ویژه z_k=x_k- y_ki   ​ وجود دارد.

plot(z, "o")

axis equal

grid on

xlabel("Re(z)")

ylabel("Im(z)")

ترسیم مجموعه‌های داده مختلط متعدد

بخش موهومی را در برابر بخش حقیقی دو مجموعه داده مختلط ترسیم کنید. اگر چندین آرگومان ورودی مختلط را به plot بدهید، مانند plot(z1, z2)، تابع plot بخش موهومی را نادیده می‌گیرد و فقط بخش حقیقی ورودی‌ها را ترسیم می‌کند. برای ترسیم بخش حقیقی در برابر بخش موهومی برای چندین ورودی مختلط، باید به طور صریح بخش حقیقی و بخش موهومی را به plot بدهید.

به عنوان مثال، دو بردار مختلط z1 و z2 ایجاد کنید.

x = -2:0.25:2;

z1 = x.^exp(-x.^2);

z2 = 2*x.^exp(-x.^2);

دانلود کنید: آموزش کامل برنامه نویسی در متلب (22 جلسه رایگان به زبان فارسی)

بخش حقیقی و بخش موهومی هر بردار را با استفاده از توابع real و imag پیدا کنید.

re_z1 = real(z1);

im_z1 = imag(z1);

re_z2 = real(z2);

im_z2 = imag(z2);

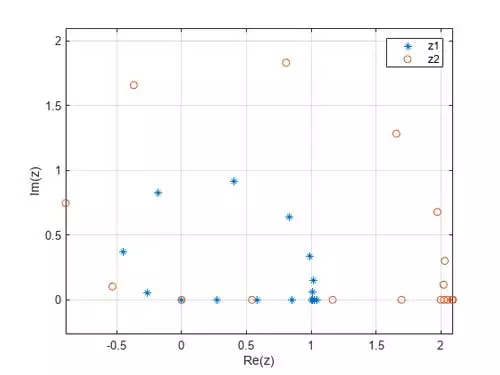
داده‌های مختلط را ترسیم کنید.

plot(re_z1, im_z1, "*", re_z2, im_z2, "o")

axis equal

grid on

legend("z1", "z2")

xlabel("Re(z)")

ylabel("Im(z)")

ویدیوی آموزشی اعداد مختلط در متلب

اینو یاد بگیرید: سیمولینک در نرم افزار متلب

ویدیوی آموزشی رسم نمودار قطبی در متلب

اینو یاد بگیرید: آموزش شبکه عصبی در متلب

در نتیجه، استفاده از اعداد مختلط در MATLAB امکانات گسترده‌ای را برای تحلیل و تجسم داده‌های مختلط فراهم می‌کند. این نرم‌افزار با ارائه توابع مختلف برای محاسبه اندازه، زاویه فاز، و اجزای حقیقی و موهومی اعداد مختلط، کار با این اعداد را ساده و کارآمد می‌سازد. همچنین، قابلیت‌های متنوع MATLAB در رسم نمودارهای دکارتی و قطبی، به کاربران امکان می‌دهد تا به‌طور دقیق و جامع داده‌های مختلط را تحلیل و ارائه کنند. از تحلیل ریشه‌های مختلط و مقادیر ویژه تا ترسیم منحنی‌های پارامتریک و داده‌های چندگانه، MATLAB ابزار قدرتمندی برای کار با اعداد مختلط در اختیار کاربران قرار می‌دهد.